Bac S 2015 Antilles Guyane
Correction © http://labolycee.org
EXERCICE I :
LES TIRS AU BUT
(6 points)
1. Schématisation du problème
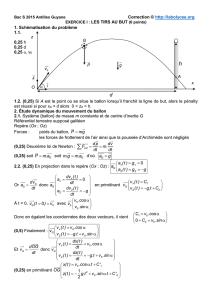
1.1.
0,25 h
0,25 d
0,25 α, v
0
1.2. (0,25) Si A est le point où se situe le ballon lorsqu’il franchit la ligne de but, alors le pénalty
est réussi si pour x
A
= d alors 0 < z
A
< h.
2. Étude dynamique du mouvement du ballon
2.1. Système {ballon} de masse m constante et de centre d’inertie G
Référentiel terrestre supposé galiléen
Repère (Ox ; Oz)
Forces : poids du ballon,
P mg
=
les forces de frottement de l’air ainsi que la poussée d’Archimède sont négligés
(0,25) Deuxième loi de Newton :
.
ext
dp dv
F m
dt dt
= =
∑
(0,25) soit
G
P m.a
=
soit
G
m.g m.a
=
d’où
G
a g
=
2.2. (0,25) En projection dans le repère (
Ox
;
Oz
) :
0
x x
GZ Z
a (t) g
a
a (t) g g
= =
= = −
Or
G
G
dv
a
dt
=
donc
0
x
x
GZ
Z
dv (t)
adt
adv (t)
a g
dt
= =
= = −
en primitivant
1
2
x
GZ
v (t) C
v
v (t) g.t C
=
= − +
À t = 0,
G
v (t ) v
= =
0
0
avec
v .cos
vv .sin
α
α
0
00
Donc en égalant les coordonnées des deux vecteurs, il vient
C v .cos
C v .sin
= α
+ = α
1 0
2 0
0
(0,5) Finalement :
0
0
x
GZ
v (t) v .cos
vv (t) g.t v .sin
= α
= − + α
Et
G
dOG
v
dt
=
donc
0
0
x
G
Z
dx(t)
v (t) v .cos
dt
vdz(t)
v (t) g.t v .sin
dt
= = α
= = − + α
(0,25) en primitivant
0 1
2
0 2
1
2
x(t) v .cos .t C'
OG
z(t) g.t v .sin .t C'
= α +
= − + α +
α
x
d
z
O
k
i
v
0
h
A
P
g
G

À t = 0, OG(t )
= =
0 0
donc en égalant les coordonnées des deux vecteurs
C'
C' =
=
1
2
0
0
(0,25) Finalement les équations horaires x(t) et z(t) sont :
0
20
1
2
x(t) v .cos .t
OG
z(t) g.t v .sin .t
= α
= − + α
Pour obtenir l’équation de la trajectoire z(x) du ballon, on isole le temps t de x(t) et on reporte
l’expression de t dans z(t) :
x = v
0
.cos
α
.t donc
x
t
v .cos
=
α
0
et
2
0
0 0
1
2x x
z(x) g. v .sin .
v .cos v .cos
= − + α
α α
(0,25)
Finalement :
2
0
. ²
( ) tan .
2. .(cos )²
g x
z x x
v
= − + α
α
2.3.
(0,25)
Le pénalty est réussi si pour
xA
= 11,0 m on a 0 <
zA
< 2,44 m.
2
2
0
.
tan .
2. .(cos )²
A
A A
g x
z x
v
= − + α
α
(
)
( ) ( )
2
2 2
9,81 11,0
tan55 11,0
2 11,5 cos55
A
z
×
= − + ×
× ×
=
2,1 m
(0,25)
Comme
zA
vérifie les inégalités 0 <
zA
< 2,44 m, le pénalty est réussi.
3. Étude énergétique du mouvement du ballon
3.1. (0,5 expressions + 0,5 raisonnement)
Énergie cinétique :
Ec =
.m.v
2
1
2
Énergie potentielle de pesanteur : E
pp
= m.g.z
Énergie mécanique : E
m
= E
c
+ E
pp
=
.m.v
2
1
2 + m.g.z
À t = 0, le ballon est à l’origine du repère donc x = 0 et z = 0.
À cette date, l’énergie potentielle de pesanteur E
PP
= m.g.z est nulle. Seule la courbe 3 passe
par l’origine du repère du graphe des énergies. Ainsi
la courbe 3 est
associée à
l’énergie
potentielle de pesanteur
.
Les frottements étant négligés, l’énergie mécanique est constante au cours du mouvement. On
associe donc
la courbe 1
à
l’énergie mécanique
.
La
courbe 2
est donc associée à
l’énergie cinétique
. La vitesse diminue lors de la montée en
altitude de la balle, puis augmente au cours de la descente.

3.2. (0,25 + 0,25) Lorsque le ballon franchit la ligne de but, x
A
= 11,0 m ; graphiquement on lit :
E
C
= 28 J et E
PP
= 13 J.
Or E
C
=
A
.m.v
2
1
2 donc
C
A
E
v
m
=
2
2
soit
C
A
E
v
m
=2
en ne conservant que la solution positive.
(0,25)
A
v,×
=
2 28
0 620
= 9,5 m.s
−1
.
Et E
PP
= m.g.z
A
= m.g.h
A
donc
PP
A
E
h
m.g
=
(0,25) soit
A
h
, ,
=×
13
0 620 9 81
= 2,1 m.
Remarque : on retrouve la valeur de z
A
de la question 2.3.
3.3. L’énergie mécanique du ballon se conserve au cours du mouvement.
(0,25) Ainsi, entre le point O et le point A on a : E
m
(O) = E
m
(A)
soit
.m.v
2
0
1
2 + m.g.z
O
=
A
.m.v
2
1
2 + m.g.z
A
Or z
O
= 0 m et z
A
= h
A
donc :
.m.v
2
0
1
2 + 0 =
A
.m.v
2
1
2 + m.g.h
A
(0,25) En multipliant tous les termes par 2 et en les divisant par m, on obtient :
v
2
0
=
A
v
2
+ 2.g.h
A
d’où :
A
v
2
=
v
2
0
– 2.g.h
A
Finalement, en ne conservant que la solution positive :
A A
v v .g.h
= −
2
0
2
(0,25) v
A
=
( )
, , ,
− × ×
2
115 2 9 81 2 1
= 9,5 m.s
−1
.
On retrouve bien la valeur v
A
de la vitesse du ballon lorsqu’il franchit la ligne de but.
La conservation de l’énergie mécanique utilisée ici est confirmée.
E
C
= 28 J
E
PP
= 13 J
1
/
3
100%