a − b

Hors-Programme : POLYN ˆ OMES - DIVISION EUCLIDIENNE
Soient aet bdeux nombres.
D’apr`es la seconde identit´e remarquable :
a2−b2= (a+b)(a−b)
Plus g´en´eralement :
a3−b3= (a−b)(a2+ab +b2)
a4−b4= (a−b)(a3+a2b+ab2+b3)
a5−b5= (a−b)(a4+a3b+a2b2+ab3+b4)
Pour tout n∈Ntel que n6=0 :
an−bn= (a−b)an−1+an−2b+an−3b2+...
···+a2bn−3+abn−2+bn−1
Propri´et´e
D´emonstrations
1. D´evelopper le membre de droite, et retrouver
l’autre membre (sommation t´el´escopique).
2. Par r´ecurrence ...
3. En utilisant la somme des termes d’une suite
g´eom´etrique :
1−qn
1−q=1+q+q2+q3+···+qn−1
Posons q=a/b:
1−(a
b)n
1−(a
b)=1+a
b+a b2+···+a bn−1
En multipliant le tout par bn−1:
– `a gauche :
bn−1×1−(a
b)n
1−(a
b)=bn
b×1−(a
b)n
1−(a
b)=bn−an
b−a
– `a droite :
bn−11+a
b+a b2+···+a bn−1
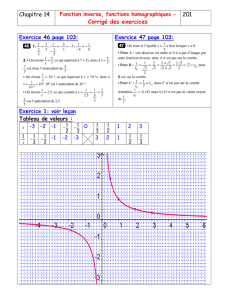
=bn−1+abn−2+a2bn−3+···+an−2b+an−1
d’o `u l’´egalit´e :
bn−an= (b−a)an−1+an−2b+an−3b2+...
···+a2bn−3+abn−2+bn−1
on obtient l’´egalit´e voulue en remarquant
que aet bjouent un rˆole sym´etrique.
Application : factorisation d’un polyn ˆome
f(x) = x3+2x2+3x−22
On remarque que f(2) = 0 :
f(2) = 8+8+6−22 =0
f(x)−f(2)est donc nul lorsque x=2.
f(x)−f(2)
= (x3+2x2+3x−22)−(23+2.22+3.2 −22)
= (x3−23) + 2(x2−22) + 3(x−2)−22 +22
= (x−2)(x2+2x+4) + 2(x−2)(x+2) + 3(x−2)
= (x−2)[x2+2x+4+2(x+2) + 3]
= (x−2)(x2+4x+11)
Finalement :
f(x) = (x−2)(x2+4x+11)
Nous venons donc de factoriser le polynˆome f(x)
par x−2. Plus g´en´eralement :
Soient fun polynˆome de degr´e net αune racine
de f, c`ad un nombre r´eel tel que f(α) = 0.
Il existe un polynˆome gde degr´e n−1 tel que :
f(x) = (x−α)×g(x)
Th´eor`eme
D´emonstration
f(x) = anxn+an−1xn−1+an−2xn−2+···+a1x+a0
f(α) = 0, et f(x)−f(α)est nul lorsque x=α.
f(x)−f(α)
= (anxn+an−1xn−1+an−2xn−2+···+a1x+a0)
−(anαn+an−1αn−1+an−2αn−2+···+a1α+a0)
=an(xn−αn) + an−1(xn−1−αn−1)
+···+ap(xp−αp) + ···+a1(x1−α1)
D’apr`es la propri´et´e, quelque soit p∈Ntel que
p6=0, on peut factoriser (xp−αp)par (x−α)donc
il existe un certain polyn ˆome g(x)tel que :
f(x)−f(α) = (x−α)×g(x)

Exemple
f(x) = ax3+bx2+cx +d
Si pour tout x∈R,f(x) = 0, alors :
a=b=c=d=0
En effet, pour x=0, puis x=1, puis x=−1, puis
x=2, on obtient le syst`eme :
a+b+c+d=0
−a+b−c+d=0
8a+4b+2c+d=0
d=0
On en d´eduit : a=b=c=d=0.
Plus g´en´eralement :
1. Un polyn ˆome est nul si et seulement si tous
ses coefficients sont nuls.
2. Deux polynˆomes sont ´egaux si et seule-
ment si ils ont les mˆemes coefficients.
Th´eor`eme
D´emonstration
1. Consid´erons un polynˆome :
f(x) = anxn+an−1xn−1+···+a1x+a0
Si f(x) = 0 pour tout x∈R, alors en parti-
culier f(0) = 0 et donc a0=0. Mais dire que
f(0) = 0 signifie que 0 est une racine de f;
on peut donc factoriser f(x)par x−0=x:
f(x) = x×anxn−1+an−1xn−2+···+a1
Mais f(x) = 0 pour tout x∈R, et on en
d´eduit que pour tout x∈R,
anxn−1+an−1xn−2+···+a1=0
On recommence : pour x=0, a1=0, etc.
2. Consid´erons deux polynˆomes :
f(x) = anxn+an−1xn−1+···+a1x+a0
g(x) = bnxn+bn−1xn−1+···+b1x+b0
On peut supposer fet gde mˆeme degr´e n,
quitte `a autoriser des coefficients nuls.
f(x)−g(x)
= (an−bn)xn+ (an−1−bn−1)xn−1+...
···+ (a1−b1)x+ (a0−b0)
Pour tout x∈R,f(x)−g(x) = 0.
Autrement dit, le polynˆome f−gest nul.
D’apr`es le point 1, tous ses coefficients sont
nuls : an−bn=0, an−1−bn−1=0, . . .,
a1−b1=0 et a0−b0=0.
M´ethode des coefficients ind´etermin´es
Exemple 1
f(x) = x3−2x2+x+4
On remarque que f(−1) = 0. Par factorisation, il
existe un polynˆome gde degr´e 2 tel que :
f(x) = (x−(−1)) ×g(x) = (x+1)×g(x)
Posons g(x) = ax2+bx +cet remplac¸ons :
x3−2x2+x+4= (x+1)×(ax2+bx +c)
=ax3+bx2+cx +ax2+bx +c
=ax3+ (b+a)x2+ (b+c)x+c
D’apr`es le th´eor`eme pr´ec´edent :
1=a−2=b+a1=b+c4=c
On en d´eduit que (a,b,c) = (1, −3, 4):
g(x) = x2−3x+4f(x) = (x+1)(x2−3x+4)
Exemple 2
f(x) = 2x4−3x3+2x2−5x−6
On remarque que f(2) = 0. Par factorisation, il
existe un polynˆome gde degr´e 3 tel que :
f(x) = (x−2)×g(x)
Posons g(x) = ax3+bx2+cx +det remplac¸ons :
2x4−3x3+2x2−5x−6
= (x−2)×(ax3+bx2+cx +d)
=ax4+ (b−2a)x3+ (c−2b)x2+ (d−2c)x−2d
D’apr`es le th´eor`eme pr´ec´edent :
a=2
b−2a=−3
c−2b=2
d−2c=−5
−2d=−6
⇒g(x) = 2x3+x2+4x+3
f(x) = (x−2)(2x3+x2+4x+3)
Cette m´ethode d’identification est efficace, mais il
existe une autre m´ethode, encore plus rapide.

Division euclidienne de polyn ˆomes
Rappel / division euclidienne
1. Divisons 34 par 5 ; le dividende est a=34,
et le diviseur est b=5.
34 5
−30 6
4
a=b×q+r
34 =5×6+4
Le quotient est q=6 et il reste r=4<5.
Ici, on peut dire que 5 ne divise par 34
puisque le reste n’est pas nul.
2. Divisons 45 par 9 ; le dividende est a=45,
et le diviseur est b=9.
45 9
−45 5
0
a=b×q+r
45 =9×5+0
Le quotient est q=5 et il reste r=0<9.
Ici, on peut dire que 9 divise 45 puisque le
reste est nul.
Exemple 1 / avec des polyn ˆomes
f(x) = x3+x2+x+1
On v´erifie facilement que f(−1) = 0.
Il existe donc un polyn ˆome gtel que :
f(x) = (x−(−1)) ×g(x) = (x+1)×g(x)
Pour trouver g(x), il suffit de poser la division
euclidienne de f(x)par (x+1):
x3+x2+x+1x+1
−(x3+x2)x2+1
0+x+1
−(x+1)
0
Comme le reste est nul, x+1 divise bien f(x)et :
f(x) = (x+1)(x2+1)
Exemple 2
f(x) = x4+5x3−18x2−25x+21
On v´erifie que f(3) = 0 et que f(−7) = 0. Il existe
un polynˆome gde degr´e 4 −1−1=2 tel que :
f(x) = (x−3)×(x−(−7)) ×g(x)
Pour d´eterminer g, il suffit de diviser deux fois :
x4+5x3−18x2−25x+21 x−3
−(x4−3x3)x3+8x2
8x3−18x2+6x−7
−(8x3−24x2)
6x2−25x
−(6x2−18x)
−7x+21
−(−7x+21)
0
f(x) = (x−3)×(x3+8x2+6x−7)
On sait que −7 est aussi racine de f, or ce n’est
pas une racine de (x−3), donc −7 est racine
de (x3+8x2+6x−7); il nous faut donc diviser
(x3+8x2+6x−7)par (x+7)pour trouver g(x):
x3+8x2+6x−7x+7
−(x3+7x2)x2+x−1
x2+6x
−(x2+7x)
−x−7
−(x+7)
0
Ce qui donne la factorisation souhait´ee :
f(x) = (x−3)×(x+7)×(x2+x−1)
Soit fun polyn ˆome :
f(x) = anxn+an−1xn−1+···+a1x+a0
Si α1, . . . , αpsont pracines distinctes de f, alors
on peut factoriser fsous la forme :
f(x) = (x−α1)× ··· × (x−αp)×g(x)
o `u gest un polynˆome de degr´e n−p.
Th´eor`eme 
factorisations succesives
Cons´equences
– Un polynˆome non-nul de degr´e nadmet au
maximum nracines.
– Si un polyn ˆome de degr´e nadmet n+1 racines,
alors ce polynˆome est le polynˆome nul.

In´equations polynˆomiales
Exemple
x4+5x3−18x2−25x+21 ≥0
Son membre de gauche est le polynˆome :
f(x) = x4+5x3−18x2−25x+21
Pour r´esoudre cette in´equation, il suffit de factori-
ser f; d’apr`es ce qui pr´ec`ede, il faut donc r´esoudre :
(x−3)×(x+7)×(x2+x−1)≥0
Le trinˆome x2+x−1 a pour discriminant ∆=
1+4=5>0 donc deux racines distinctes :
x1=−1−√5
2x2=−1+√5 2
x−∞−7x10x23+∞
x−3− − − − − 0+
x+7−0+ + + + +
x2+x+1+ + 0− − 0+ +
f(x) + 0−0+0+0−0+
f(x)≥0 ssi x∈]−∞;−7]∪[x1;x2]∪[3; +∞[
Fractions rationnelles
Une fraction rationnelle est :
f:x7→ P(x)
Q(x)
avec Pet Qdeux polyn ˆomes.
D´efinition
Remarque fest d´efinie sur Rpriv´e de
l’ensemble des racines de Q.
Exemple
f(x) = 3x+2
x−8
Le domaine de d´efinition de fest l’ensemble des x
qui n’annullent pas x−8.
x−8=0 ssi x=8
On en d´eduit que :
Df=R− {8}
Soit fune fraction rationnelle :
f(x) = P(x)
Q(x)
deg P=mdeg Q=n
Si m≥n, il existe deux polyn ˆomes Ret S:
f(x) = R(x) + S(x)
Q(x)
avec : deg R=m−ndeg S<n
Th´eor`eme
Exemple
f(x) = x3+x2
x+2
On peut bricoler le num´erateur :
f(x) = x3+2x2−x2−2x+2x+4−4
x+2
=x2(x+2)−x(x+2) + 2(x+2)−4
x+2
=x2−x+2−4
x+2
On obtient la forme voulue avec :
R(x) = x2−x+2 deg R=3−1=2
S(x) = −4 deg S=0<1
On peut retrouver R(x)et S(x)plus efficacement :
par division euclidienne !
x3+x2x+2
−(x3+2x2)x2−x+2
−x2
−(−x2−2x)
2x
−(2x+4)
−4
x3+x2= (x+2)×(x2−x+2) + (−4)
Puis on divise tout par x+2 :
f(x) = x2−x+2−4
x+2