Rappel – les règles pour les nombres entiers

Rappel – les règles pour les nombres entiers
1) Addition :
a) Si c’est le même signe, additionner et garder le signe.
Ex. (-3) + (-4) = -7 Ex. (+9) + (+12) = +21
b) Si les signes sont différents, soustraire le plus petit chiffre du plus grand,
puis garder le signe du plus grand.
Ex. (-13) + (+4) = -9 Ex. (+9) + (-12) = -3
2) Soustraction :
a) Changer à une addition, en changeant la soustraction à une addition et
changer le signe du deuxième chiffre, puis résoudre.
Ex. (-9) – (-4) = (-9) + (+4) = -5 Ex. (4) – (6) = (4) + (-6) = -2
3) Multiplication et Division :
a) même signe = réponse positive! Ex. (-7)(-8) = +56
b) signe opposé = réponse négatif! Ex. (50) ÷ (-5) = -10
Pratique :
(-13) + (-40) = (+19) + (+112) =
(-7) + (-8) = (-5)(-60) =
(-13) + (+4) = (-70) - (-18) =
(+19) + (-12) = (+105) ÷ (-5) =
(-9) – (-4) = (4) – (6) =
(50) ÷ (-5) = (19) – (21) =
(-9) – (-4) = (14) – (6) =

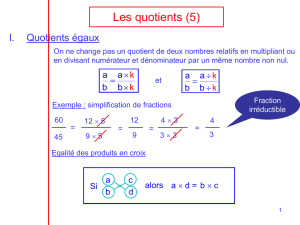
Rappel – les règles pour les fractions
1) Addition & Soustraction :
a) Trouver le plus petit commun multiple pour les dénominateurs.
b) Multiplier les numérateurs par le même chiffre que le dénominateur,
puis mettre les deux numérateurs sur le dénominateur commun et
simplifier.
Ex. 
, Le plus petit commun multiple de 4 et 6 est 12.
 =   =   = 
Ex. 
, Le plus petit commun multiple de 3 et 5 est 15.
 =   =   = 
2) Multiplication : Multiplier les numérateurs, multiplier les dénominateurs,
simplifier.
Ex : 
3) Division :
Méthode A : Trouver les dénominateurs communs, puis diviser les numérateurs et
diviser les dénominateurs.
Ex.
 = 
Méthode B : Laisser la première fraction, changer la division à une multiplication,
et inverser la deuxième fraction.
Ex.