Rochambeau. 2016. Enseignement spécifique. Corrigé

Rochambeau. 2016. Enseignement spécifique. Corrigé
EXERCICE 1
Partie A
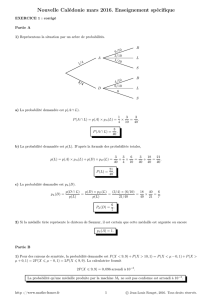
1) L’énoncé donne P(V) = 0, 96,P(A) = 0, 6 et PA(V) = 0, 98. Représentons la situation par un arbre de probabilités.
A
B
0, 6
0, 4
V
V
V
V
0, 98
0, 02
La probabilité demandée est P(A∩V).
P(A∩V) = P(A)×PA(V) = 0, 6 ×0, 98 =0, 588.
2) D’après la formule des probabilités totales, P(V) = P(A∩V) + P(B∩V)et donc
P(B∩V) = P(V) − P(A∩V) = 0, 96 −0, 588 =0, 372.
Ensuite,
PB(V) = P(B∩V)
P(B)=0, 372 0, 4 =0, 93.
3) La probabilité demandée est PV(B).
PV(B) = PV∩B
p(V)=P(B) − P(V∩B) 1− (P(A∩V) + P(B∩V)) =0, 4 −0, 372 1− (0, 372 +0, 588)=0, 028 0, 0, 04 =0, 7.
Le technicien a donc raison.
Partie B
1) La probabilité demandée est P(0, 9 6X61, 1). La calculatrice fournit P(0, 9 6X61, 1) = 0, 9309 . . . ou encore
P(0, 9 6X61, 1) = 0, 93 au centième près.
D’autre part, PB(V) = P(B∩V)
P(B)=0, 372 0, 4 =0, 93. Donc, la probabilité qu’une bille produite par la machine B soit
vendable est bien égale au centième près à celle de la partie A.
2) 0, 9 6Y61, 1 ⇔−0, 1 6Y−160, 1 ⇔−0, 1
σ′6Y−1 σ′60, 1 σ′. On sait que la variable Z=Y−1 σ′suit la loi
normale centrée réduite et de plus, P(0, 9 6Y61, 1) = P−0, 1
σ′6Z60, 1 σ′. Ensuite, pour des raisons de symétries,
PZ60, 1
σ′=P−0, 1 σ′6Z60, 1 σ′+PZ6−0, 1 σ′=0, 98 +0, 02 2=0, 99.
La calculatrice fournit
PZ60, 1
σ′=0, 99 ⇔0, 1 σ′=2.3263 . . . ⇔σ′=0, 0429 . . .
Donc, σ′=0, 043 arrondi à 10−3.
http ://www.maths-france.fr 1 c Jean-Louis Rouget, 2016. Tous droits réservés.

Partie C
1) a) Notons Xla variable aléatoire égale au nombre de billes noires dans le sachet.
•40 expériences identiques et indépendantes sont effectuées.
•chaque expérience a deux issues à savoir « la bille est noire » avec une probabilité p=1
5et « la bille n’est pas
noire » avec une probabilité 1−p=4
5.
Xsuit donc une loi binomiale de paramètres n=40 et p=1
5. La probabilité demandée est P(X=10). On sait que
P(X=10) = 40
101
510 4 540−10
=0, 107 arraondi à 10−3
(fourni par la calculatrice).
b) Déterminons un intervalle de fluctuation asymptotique au seuil 95%. Ici, n=40 et p=1
5=0, 2. On note que
n>30,np =8et n(1−p) = 32 de sorte que np >5et n(1−p)>5. Un intervalle de fluctuation est
"p−1, 96rp(1−p)
n, p +1, 96rp(1−p) n#="0, 2 −1, 96r0, 2 ×0, 8 40 , 0, 25 +1, 96r0, 2 ×0, 8 40 #= [0, 07;0, 33]
en arrondissant de manière à élargir un peu l’intervalle. La fréquence observée est f=12
40 =0, 3. Cette fréquence
appartient à l’intervalle de fluctuation et donc on ne peut pas remettre en cause le réglage de la machine qui teinte les
billes.
2) Soit nle nombre de billes dans un sachet. Le nombre de billes noires de ce sachet est une variable aléatoire Xqui
suit une loi binomiale de paramètres net p=0, 2. La probabilité que le sachet contienne au moins une bille noire est
P(X>1) = 1−P(X=0) = 1− (0, 8)n.
Par suite,
P(X>1)>0, 99 ⇔1− (0, 8)n>0, 99 ⇔0, 01 >(0, 8)n⇔(0, 8)n60, 01
⇔ln ((0, 8)n)6ln(0, 01) (par stricte croissance de la fonction ln sur ]0, +∞[)
⇔nln(0, 8)6ln(0, 01)⇔n>ln(0, 01)
ln(0, 8)(car ln(0, 8)< 0)
⇔n>20, 6 . . .
⇔n>21 (car nest un entier).
Le nombre minimal de billes que doit contenir un sachet pour avoir une probabilité supérieure à 0, 99 d’avoir au moins
une bille noire est 21.
http ://www.maths-france.fr 2 c Jean-Louis Rouget, 2016. Tous droits réservés.

EXERCICE 2
Partie A
1) f(xB) = f(2e) = 2e ln 2e
2−2e +2=2e −2e +2=2=yB. Donc, le point Bappartient à la courbe Cf.
f(xI) = f(2) = 2e ln 2
2−2+2= −2+2=0=yI. Donc, le point Iappartient à la courbe Cf.
La fonction fest dérivable sur [2, 2e]et pour tout xde [2, 2e],
f′(x) = 1×ln x
2+x×1/2 x/2 −1=ln x 2+1−1=ln x 2.
Par suite, f′(xI) = ln 2
2=ln(1) = 0. On en déduit que l’axe des abscisses est tangent à la courbe Cfen I.
2) a) On a déjà xB=2e et f(xB) = 2. Ensuite, f′(xB) = f′(2e) = ln 2e
2=ln(e) = 1. Une équation de la tangente
àCfau point Best y=2+1×(x−2e)ou encore y=x+2−2e.
Ensuite, x+2−2e =0⇔x=2e −2. Le point Da donc pour coordonnées (2e −2, 0).
b) L’aire, exprimée en m2, du triangle ABI vaut AB ×AI
2ou encore (2e −2)×2 2ou enfin 2e −2.
L’aire, exprimée en m2, du trapèze AIDB vaut (AB +ID)×AI
2ou encore ((2e −2) + (2e −4)) ×2 2ou enfin 4e −6.
On en déduit que
2e −26S64e −6.
Ceci fournit pour le volume V, exprimé en m3, de la cuve :
10e −10 6V620e −30.
Ceci fournit encore 17, 1 6V624, 4.
3) a) La fonction Gest dérivable sur [2, 2e]et pour tout xde [2, 2e],
G′(x) = 2x
2ln x 2+x2 2
1/2
x/2 −2x 4=xln x 2+x 2−x 2=xln x 2=g(x).
Donc, la fonction Gest une primitive de la fonction gsur [2, 2e].
b) Une primitive de la fonction fsur [2, 2e]est alors la fonction F:x7→x2
2ln x 2−x2 4−x2 2+2x ou encore
F:x7→x2
2ln x 2−3x2 4+2x
c)
S=Z2e
2
(2−f(x)) dx =2x −x2
2ln x 2−3x2 4+2x2e
2
= − (2e)2
2ln 2e 2−3(2e)2 4+22 2ln 2 2−3×22 4
= −2e2+3e2−3=e2−3,
puis
V=5e2−3=22 m3arrondi au mètre cube.
Partie B
1) Notons V0le volume cherché.
La fonction fest continue sur [2, 2e]et croît strictement de 0à2sur cet intervalle. Donc, existe un réel x0et un seul
dans l’intervalle [2, 2e]tel que f(x0) = 1.
La calculatrice fournit f(4, 3) = 0, 99 . . . < 1 et f(4, 4) = 1, 06 . . . > 1. Puisque la fonction fest croissante sur [2, 2e],
on en déduit que 4, 3 6x064, 4.
http ://www.maths-france.fr 3 c Jean-Louis Rouget, 2016. Tous droits réservés.

Quand xaugmente, la hauteur d’eau dans la cuve augmente puis le volume d’eau dans la cuve augmente. Donc, la
fonction vest croissante sur [2, 2e]. On en déduit que
v(4, 3)6V06v(4, 4).
La calculatrice fournit v(4, 3) = 7, 3 . . . et v(4, 4) = 8, 2 . . . et on en déduit que V0=8m3au m3près.
2) L’algorithme affiche une valeur approchée de la hauteur d’eau dans la cuve pour laquelle le volume d’eau dans la
cuve vaut la moitié du volume total à 10−3près.
http ://www.maths-france.fr 4 c Jean-Louis Rouget, 2016. Tous droits réservés.

EXERCICE 3
1) |1+i|=√12+12=√2puis
1+i=√21
√2+1 √2i=√2cos π
4+isin π 4=√2eiπ
4.
2) Graphique.
1
2
3
4
5
−1
−2
−3
−4
−5
−6
−7
−8
12345−1−2−3−4−5
A
B
C
D
O
M0
M1
M2 M3
M4
M5
M6
Soit nun entier naturel. La plus grande distance du point Oà un point du carré ABCD est OA =4. Donc, on est sûr
que le point Mnest à l’extérieur du carré si OMn> 4.
OMn> 4 ⇔|zn|> 4 ⇔|1+i|n> 4 ⇔√2n
> 4
⇔ln √2n>ln(4) (par stricte croissance de la fonction ln sur ]0, +∞[)
⇔nln √2> 2 ln(2)⇔n
2ln(2)> 2 ln(2)⇔n 2> 2 ⇔n > 4
⇔n>5.
Donc, l’entier n0=5convient. On note que, puisque M4=C,5est la plus petite valeur possible de n0.
http ://www.maths-france.fr 5 c Jean-Louis Rouget, 2016. Tous droits réservés.