N° 1 1ère méthode : utilisation des ions nitrate 1.1 La réaction de

Document1
N°
1
1ère méthode : utilisation des ions nitrate
1.1
La réaction de synthèse du diiode est une réaction d’oxydoréduction :
Couple SO42–(aq) / HSO3–(aq)
oxydation HSO3–(aq) + H2O(l) = SO42–(aq) + 2e– + 3H+(aq)
que l’on peut écrire (1) HSO3–(aq) + 4H2O(l) = SO42–(aq) + 2e– + 3H3O+(aq)
Couple IO3–(aq) / I2(aq)
réduction 2IO3–(aq) + 10e– + 12H+(aq) = I2(aq) + 6H2O(l)
que l’on peut écrire (2) 2IO3–(aq) + 10e– + 12H3O+(aq) = I2(aq) + 18H2O(l)
En faisant la somme 5(1) + (2), on retrouve l’équation de la réaction de synthèse : (non exigé)
5HSO3–(aq) + 20H2O(l) = 5SO42–(aq) + 10e– + 15H3O+(aq)
2IO3–(aq) + 10e– + 12H3O+(aq) = I2(aq) + 18H2O(l)
2IO3–(aq) + 5HSO3–(aq) + 2H2O(l) = 5SO42–(aq) + I2(aq) + 3H3O+(aq)
1.2.1
Qr,éq = K =
5
3
2
3
3
32
52
4
][][
][][][
eqeq
eqeqeq
HSOIO
OHISO
1.2.2
[H3O+] intervient dans la valeur du quotient de réaction Qr (Qr =
5
3
2
3
3
32
52
4
][][
][][][
HSOIO
OHISO
)
Si on abaisse le pH, la concentration en ions oxonium du système augmente (car pH = – log[H3O+])
Ce qui implique une augmentation du quotient de réaction Qr, lequel devient plus grand que le quotient de réaction à
l’équilibre Qr,éq. ( Qr > Qr,éq )
Il y a donc déplacement de l’équilibre dans le sens indirect, ce qui permet d’obtenir moins de diiode.
Ce n’est donc pas une bonne initiative pour la production de diiode…
2
2nde méthode : action de l’eau oxygénée sur les ions iodure
2.1.1
Équation
H2O2 (aq) + 2 I- (aq) + 2 H3O+(aq) = I2 (aq) + 4 H2O (l)
État du
système
avancement
en mol
Quantités de matières en mol
initial
x = 0
cC.VC
cB.VB
cA.VA
0
beaucoup
intermédiaire
x
cC.VC – x
cB.VB –2x
cA.VA –2x
x
beaucoup
Final réel
xf
cC.VC – xf
cB.VB –2xf
cA.VA –2xf
xf
beaucoup
Final si
réaction
totale
xmax
cC.VC – xmax
cB.VB –2 xmax
cA.VA –2xmax
xmax
beaucoup
Si H2O2 est le réactif limitant alors cC.VC – xmax = 0 donc xmax = cC.VC
soit xmax = 0,1010,010–3 = 1,010–3 mol
Si I– est le réactif limitant alors cB.VB –2 xmax = 0 donc xmax =
.
2
BB
cV
soit xmax =
3
0,10 60 10
2
= 3,010–3 mol
Si H3O+ est limitant alors cA.VA –2 xmax = 0 donc xmax =
.
2
AA
cV
,
soit xmax =
3
0,10 30 10
2
= 1,510–3 mol. Expression pour H3O+ obligatoire
Le réactif limitant est celui qui conduit à la valeur de l’avancement maximal la plus faible, il s’agit donc du peroxyde
d’hydrogène H2O2 et on a xmax = 1,010–3 mol.
2.1.2
Af = k [I2]f =
)( CBA
f
VVV
x
k
donc
k
VVVA
xCBAf
f
)( 
Taux d’avancement final
max
x
xf
max
)(
xk
VVVA CBAf

Document1
3
10.0,194
100,094,0
= 1,0 A 1200 s, la transformation est totale
2.1.3
A = k [I2] =
)( CBA VVV x
k
Finalement
x
A
=
A B C
VVV
k
, avec VA,VB,VC et k constants donc le rapport x/A est
constant
2.1.4
Pour t = 1200 s, on a x = xf = 1,010–3 mol et Af = 0,94.
r =
x
A
=
A B C
VVV
k
=
94
1000,0
= 1,110–3 mol
2.1.5
v =
1.dx
V dt
et on a vu que x = r.A donc v =
1 ( . )
.d r A
V dt
avec r = constante, et V = VA + VB + VC (volume du mélange réactionnel (constant))
soit v =
.
r dA
V dt
2.1.6
la vitesse est proportionnelle à
dA
dt
(ou varie comme cette dérivée)
dA
dt
est égale au coefficient directeur de la tangente à la courbe représentative de A en fonction du temps.
On trace les tangentes en t = 200 s et en t = 800 s.
La tangente à la courbe en t = 200 s est plus verticale que celle en t = 800 s, donc
200 800tt
dA dA
dt dt
Finalement
v(t = 200 s) > v(t = 800 s).
2.1.7
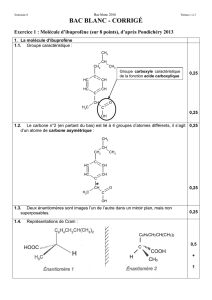
Le temps de demi-réaction est la durée nécessaire pour que l’avancement de la réaction atteigne la moitié de sa valeur
finale. x (t1/2) = xf / 2.
A est proportionnelle à x (voir 2.1.3), donc A(t1/2) = Af /2.
Graphiquement on trouve t1/2 = 7101 s.
2.2.1
VB a été divisé par deux, ainsi la quantité de matière d’ions iodure a été divisée par deux.
Les autres quantités de matière de réactifs restent inchangées.
Le volume total de la solution n’a pas changé.
Conclusion :
2 2( ) 2 2( )
exp1 exp2
aq aq
H O H O
33
exp1 exp2
H O H O
0,100 0,3010,0 '
'
][ 2exp
VeauVVV
VC
I
CBA
BB
= 3,0 x 10-2 mol.L-1
Le paramètre cinétique modifié ici est la concentration en réactif ion iodure
2.2.2
valeur de l’avancement final qui correspond à la nouvelle quantité de matière de I– :
Si I– est le réactif limitant alors cB.VB –2 xmax = 0 donc xmax =
.
2
BB
cV
soit xmax =
3
0,10 30 10
2
= 1,510–3 mol.
En reprenant les résultats du 2.1.1. pour le peroxyde d’hydrogène et les ions oxonium, on conclut que le réactif limitant
n’a pas changé.
Il s’agit encore du peroxyde d’hydrogène H2O2 et on a xmax = 1,010–3 mol.
2.2.3 a
A l’équivalence, le réactif titrant a été ajouté de manière suffisante pour être limitant simultanément avec le réactif titré.
La réaction étant totale, les quantités de matière de ces deux réactifs sont nulles à l’état final de cette situation.
2.2.3 b
Pour l’équivalence, à l’état final :
[I2]Vp – xfE = 0
Ctitrant VE – 2 xfE = 0
D’où deux reflations pour xfE. Et donc
P
Etitrant
VVC
I2 ][ 2
(ou relation équivalente)

Document1
2.2.3 c
A = k [I2] =
0,1029,3110.00,5
94
2
3
P
Etitrant
VVC
k
= 0,75
Cette absorbance est plus faible que celle obtenue à la même date dans l’expérience précédente.
La concentration en réactif I- est ici plus faible : la vitesse d’évolution du système est donc moins grande.
3
3ème méthode : électrolyse d’une solution d’acide iodhydrique
3.1.1
HI(aq) + H2O(l) = H3O+(aq) + I-(aq)
3.1.2
pH= - log[H3O+]eq =
)
00,1 100,5
log()log( 2
1
sol
V
n
= 1,3
le pH de la solution est < à ½ pKe (= 7) donc la solution est acide (pH < 7 suffit)
3.2.1
-
G A
+
3.2.2
Électrode reliée à la borne +, capte les électrons fournis par des réactions d’oxydation :
oxydation de l’eau : 2 H2O(l) = O2(g) + 4 e– + 4 H+(aq)
oxydation des anions iodure : 2 I–(aq) = I2(aq) + 2 e–
Électrode reliée à la borne –, apporte des électrons qui sont consommés par des réactions de réduction :
réduction des ions hydrogène : 2 H3O+(aq) + 2 e– = H2(g) + 2 H2O (l) (ou 2 H+(aq) + 2 e– = H2(g) )
3.2.3
Comme il n’y a pas de dégagement gazeux à l’anode, on en déduit que seule l’oxydation des anions iodure a lieu. (2I–
(aq) = I2(aq) + 2e–) Il y a production de diiode I2
À la cathode : 2H3O+(aq) + 2e– = H2(g) + 2 H2O (l) (ou 2 H+(aq) + 2 e– = H2(g) )
Il y a production de dihydrogène gazeux H2(g).
Equation chimique de l’électrolyse
2 I–(aq) + 2 H3O+(aq) = I2(aq) + H2(g) + 2 H2O (l)
(ou 2 I–(aq) + 2 H+(aq) = I2(aq) + H2(g) )
3.2.4 a
Q = I.t et Q =
e
n
.F = I.t
e
n
=
.It
F
e
n
=
4
0,25 30 60
9,65 10
e
n
= 4,710–3 mol
3.2.4 b
2H+(aq) + 2e– = H2(g), on a
2
e
n
consommée =
2
H
n
produite
2
H
n
produite =
.
2.
It
F
M
V
V
=
.
2.
It
F
(ou expression à partir de n e- )
V =
.
2.
It
F
.VM
V =
4
0,25 30 60 25
2 9,65 10
= 5,810–2 L = 58 mL de gaz H2 libéré à la cathode
cations 
 anions
ANODE
CATHODE
électrons

Document1
n°
1.1
1.2
Le régime est qualifié de pseudo-périodique car la tension uC atteint sa valeur maximale à intervalles de temps
égaux mais son amplitude diminue au cours du temps.
1.3.
4,5T = 30 – 10 = 20 ms ; T = 20/4,5 = 4,4 ms = 4,410–3 s ou valeur voisine
f = 1/T ; f = 2,3102 Hz ou valeur voisine
1.4.1.
T0 = 2.
.LC
; T0 = 2.
6
0,50 1,0 10
; T0 = 4,410–3 s
1.4.2.
(A la précision près du tracé) , T et T0 sont égaux
2.1.
EC = ½ C.uC²
2.2.
EL = ½ L.i²
2.3.
Conditions initiales : à t = 0 s uC = E et i = 0. Ainsi EL = 0, ce qui correspond à la courbe 2 ; donc EC est la
courbe 1
OU uC est maximale, donc EC est maximale, ce qui correspond à la courbe 1. et EL est la courbe 2
2.4.
Sur la figure 4 : EC(0) = 17,5 J = 17,5.10-6 J 17,50 accepté
EC(0) =
2
1
CE2 d’où E =
C
)0(E 2 C
=
6-
6-
10
2x17,5.10
= 5,9 V
2.5.
L’énergie totale ET diminue au cours du temps.
Il y a perte d’énergie, sous forme de chaleur, dans la résistance r de la bobine, en raison de l’effet Joule. ou
formulation similaire
2.6.1.
Le dipôle D apporte au circuit de l’énergie, il compense ainsi les pertes d’énergie dues à l’effet Joule.
2.6.2.
À l’aide du dipôle D, la tension uC est parfaitement sinusoïdale, son amplitude est constante au cours du temps.
1.
Une onde mécanique progressive est la propagation d’une perturbation dans un milieu matériel sans transport
de matière.
Une onde sonore est due à la propagation de zones de compression et de dilatation de tranches d’air ; elle
nécessite un milieu matériel : c’est une onde mécanique progressive.
2.
Une onde est longitudinale lorsque la direction de la perturbation est la même que la direction de propagation
de l’onde.
3.1.
La longueur d’onde  est la distance parcourue par l’onde pendant une durée égale à la période T (ou autre
définition)
3.2.
Deux points consécutifs du milieu, dans le même état vibratoire, sont situés à une distance égale à la longueur
d’onde,(ou phrase équivalente) soit d = .
3.3.
Les deux courbes sont en phase : on voit qu’elles ont leurs maxima aux mêmes dates
3.4.
On voit que 2 périodes sont représentées par 8,8 divisions. T est représenté par 4,4 div. La base de temps est 1
ms/div. Donc T = 4,4 ms
3.5.
f = 1/T = 1/ (4,4.10-3) = 2,3.102 Hz
 = v/f soit v = .f ; AN : v = 1,5 x 2,3.102 = 3,5.102 m.s-1
OU  = vT soit v = /T ; AN : v = 1,5 / (4,4.10-3) = 3,4.102m.s-1
4.1.
La fréquence d’une onde ne dépend pas du milieu de propagation : la fréquence est inchangée
4.2.
 = v/f ; f est inchangée mais v est changée. Donc  change.
’/ v’ =  / v. d’où ’= ( v’)/ v = (1,5 x 103) / 3,5 .102 = 4,3 m
OU ’= 4,4 m si v = 3,4.102m.s-1
4.3.
d = v’ t1 ; ou t1 = d / v’ = 1,50 / 1,0.103 = 1,5.10-3 s ou 1,5 ms
4.4.
t1 / T = 1,5 / 4,4 = 0,34 ; t1 < T ; on ne peut pas avoir 2 courbes en phase comme sur la figure 6 ou
justification correcte
E

Document1
1
P
= m
g
ou
P
= -mg
z
u
A
P
= - airV
g
ou
A
P
= air V
z
u
2
Calculons
A
PP/
= m /( air V) = 130 / (1,3 x50.10-3) = 2,0.103 >> 1
La valeur du poids est environ 2000 fois plus grande que la valeur de la poussée d'Archimède.On
peut donc négliger la poussée d'Archimède devant le poids.
3
Système : Le projectile ;Référentiel : le sol , référentiel terrestre supposé galiléen
Dans le cadre de la chute libre, le projectile n'est soumis qu'à son seul poids.
La 2nde loi de Newton donne: m
a
= m
g
d’où
a
=
g
En projection selon les axes Ox et Oz du repère choisi. aX=0 et aZ=-g
4
v0x = v0 cos et v0y = v0 sin
5
Sachant que
a
= d
v
/dt, par intégration des composantes du vecteur accélération on a:
vx = cste = A et vz = - gt+ B (B est une cste)
Compte tenu des CI, on a v0 cos = A et v0 sin = 0 + B
D’où : vx = v0 cos et vz = - gt + v0 sin
6
Sachant que
v
= d
OG
/ dt, par intégration des composantes du vecteur vitesse on a :
x(t) = v0 t cosC et z(t) = -
2
1
gt2 + v0 t sinD où C et D st des cstes
CI : x(0) = 0 et z(0) = H ; donc C = 0 et D = H
D’où : x(t) = v0 t cos et et z(t) = -
2
1
gt2 + v0 t sin
7
t = x / (v0 cos)
On reporte dans z(t) ; donc z(x) = -
2
1
g
22
0
2
cosvx
+ x tan  + H
8
L’expression z(x) est de la forme ax2 + bx + c ; la trajectoire est parabolique
Fig 1 allure trajectoire
9.1
Ici  = 0 ; l’équation de la trajectoire devient z(x) = -
2
1
2
0
2
v
x
+ H
L’abscisse de son point de chute est telle que z=0, soit 0 = -
2
1
2
0
2
v
x
+ H ou x2 =
gHv2
0
2
D’où x = v0
g
H2
9.2
D’après la question précédente, on a v0 = x
H
g
2
AN : si x = 100 m, alors v0 = 70 m.s-1