EXERCICE I Chimie et mouvement pour un projet scientifique (5,5

Nouvelle Calédonie Novembre 2007 Correction © http://Labolycee.org
EXERCICE I. CHIMIE ET MOUVEMENT POUR UN PROJET SCIENTIFIQUE (5,5 points)
Calculatrice interdite
1. Étude de la transformation chimique
1.1. Couple H+(aq) / H2(g) réduction 2H+(aq) + 2 e– = H2(g) (1)
Couple Mg2+(aq) / Mg(s) oxydation Mg(s) = Mg2+(aq) + 2 e– (2)
en additionnant (1)+(2) on retrouve l’équation : Mg (s) + 2 H+ (aq) = Mg2+ (aq) + H2 (g)
1.2. Quantité de matière initiale des réactifs :
n0(Mg) =
Mg
m
M
n0(Mg) =
2
0 12 12 10
24 24
,
= 0,5010–2 = 5,010–3 mol
n0(H+) = C  V
n0(H+) = 0,50  4010–3 = 2010-3 mol = 2,010–2 mol
Avancement
en mol
Mg (s) + 2 H+ (aq) = Mg2+ (aq) + H2 (g)
État initial
x = 0
5,010–3
2,010–2
0
0
En cours de
transformation
x
5,010–3 – x
2,010–2 – 2 x
x
x
État final
x = xmax
5,010–3 – xmax
2,010–2 – 2 xmax
xmax
xmax
Si Mg est limitant alors : 5,010–3 – xmax = 0 soit xmax = 5,010–3 mol
Si H+ est limitant alors : 2,010–2 – 2 xmax = 0 soit xmax =
2
2 0 10
2
,
= 1,010–2 mol
Le réactif limitant est celui qui conduit à l'avancement maximal le plus faible : il s'agit du magnésium et on
vérifie bien que xmax = 5,010–3 mol.
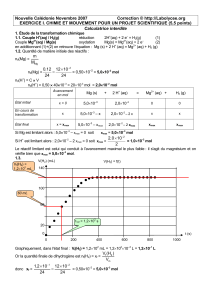
1.3.
Graphiquement, dans l'état final : Vf(H2) = 1,2102 mL = 1,210210–3 L = 1,210–1 L
Or la quantité finale de dihydrogène est nf(H2) = xf =
f2
m
V (H )
V
donc xf =
12
12 10 12 10
24 24
,
= 0,5010–2 = 5,010–3 mol
V(H2) (mL)
V(H2) = f(t)
t (s)
140
100
60
20
0
0 200 400 600 800 1000
Vf(H2) =
1,2102 mL
60 mL
t1/2 = 1,2102 s

1.4. On a xf = xmax donc
f
max
x
x
= 1,0 : la transformation est totale.
1.5. Le temps de demi-réaction t1/2 est la durée pour laquelle l'avancement atteint la moitié de sa valeur
finale : x(t1/2) =
f
x
2
.
Ici, l'avancement est proportionnel au volume de dihydrogène , x =
2
m
V(H )
V
,
donc on peut écrire : V(H2)(t1/2) =
f2
V (H )
2
Méthode: on trace la droite horizontale
2
V(H )
2
= 60 mL . Cette droite coupe la courbe V(H2) = f(t) en un point
d'abscisse égale à t1/2. Graphiquement on détermine : t1/2 = 1,2102 s
1.6. La température est un facteur cinétique. On peut placer le ballon, contenant les réactifs, dans un bain
d'eau glacée. L'état final sera atteint moins rapidement ce qui augmentera le temps de demi-réaction t1/2.
Remarque : la concentration en réactif est aussi un facteur cinétique. On peut augmenter le temps de
demi-réaction t1/2 en diminuant la concentration initiale de la solution d'acide chlorhydrique mais en
conservant le métal magnésium comme réactif limitant afin d'avoir le même état final.
2. Étude du mouvement ascendant d'une bulle de dihydrogène
2.1. Évolution de la vitesse au cours du temps
2.1.1. Le régime R2 est le régime permanent.
2.1.2.
2.2. Bilan des forces
2.2.1. La valeur de la poussée d'Archimède est égale au poids du fluide déplacé (ici de l’eau).
= meau.g = 0 . Vb . g
2.2.2. Expression de la valeur P du poids de le bulle : P = m . g =  . Vb . g
Ainsi
b
0 b 0
Vg
PVg
..
..
2
3
P 8 3 10
10 10
,
,
= 8,3  10–5
P
<<1 donc P <<
On peut effectivement négliger le poids de la bulle devant la poussée d'Archimède.
Figure 3
0 0,2 0,4 0,6 0,8
t(s)
Évolution de la valeur de la vitesse de la bulle au
cours du temps
v (m.s-1)
0,35
0,3
0,25
0,2
0,15
0,1
0,05
0
R1
R2
vlim = 0,29 m.s-1
on voit que vlim < 0,3 m.s-1
sans calculs :  << 0 donc
0
<< 1

2.2.3. Pour deux dates proches ti+1 et ti–1 encadrant la date ti, le vecteur accélération est défini par
i+1 i-1
i11
v(t ) v(t )
a(t ) ii
tt
Pendant le régime R1, la vitesse de la bulle augmente et le mouvement est ascendant. Alors v(ti+1) > v(ti–1) et
le vecteur accélération est donc vertical vers le haut comme le vecteur
11 ii
v(t ) v(t )
.
D’après la deuxième loi de Newton, appliquée au système bulle, dans un référentiel terrestre supposé
galiléen,
  f m.a
. Donc le vecteur
f
est vertical vers le haut.
Voir figures ci-dessous. La représentation (a) n’est pas correcte, la représentation (c) est correcte.
D’autre part, la poussé d'Archimède est une force verticale orientée vers le haut cela exclut la
représentation (b).
La seule représentation possible des forces est la représentation (c).
2.2.4. Lorsque le régime permanent R2 est atteint, la valeur de la vitesse est constante et égale à vlim.
Le mouvement de la bulle étant rectiligne, le vecteur vitesse
v
est un vecteur constant donc le vecteur
accélération
dv
a0
dt
. La deuxième loi de Newton impose alors
f0  
. Les forces se compensent.
On peut aussi utiliser la première loi de Newton (principe d’inertie)
3. Étude du mouvement vertical d'une bille d'acier dans l'air
3.1. Une fois lancée, la bille d'acier n'est soumise qu'à la force poids : il s'agit donc
d'un mouvement de chute libre.
3.2. Le système bille est étudié dans un référentiel terrestre supposé galiléen. Le
repère est un axe (Oy) vertical et dirigé ver le bas.
La deuxième de Newton donne
P
= m.
a
m.
g
= m.
a
Soit
a
=
g
En projection sur (Oy) : ay = g
y
dv
dt
= g
donc en primitivant, il vient vy(t) = g.t + Cte
Or à t = 0 s, vy(0) = v0y donc Cte = v0y
Finalement vy(t) = g.t + v0y
j
O
y
0
v
P
g
G
1i
v(t )
1i
v(t )
11 ii
v(t ) v(t )
a
b
c
f
f
FAUSSE
FAUSSE
CORRECTE
f
f
f
f
f

3.3. a) "La bille est lâchée sans vitesse initiale" correspond à la courbe (2) pour laquelle vy(0) = 0 m.s-1.
b) "La bille est lancée verticalement vers le haut"
correspond au cas pour lequel v0y est négatif, il s'agit de la courbe (3).
c) "La bille est lancée verticalement vers le bas"
correspond au cas pour lequel v0y est positif, il s'agit de la courbe (1).
4. La présentation orale du projet scientifique
« Arthur : – l’objet lourd tombera plus vite que l’objet léger. »
La réponse d'Arthur est erronée car la coordonnée verticale de la vitesse de l'objet , vy(t) = g.t + v0y , est
indépendante de la masse. Les deux billes tomberont avec la même vitesse dans le tube où règne le vide.
O
y
O
y
0
v 2 j.
0
v 2 j.
j
j