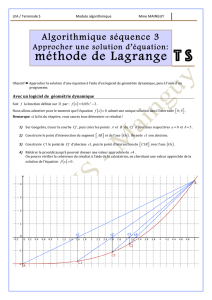
TP7 | Résolution approchée d`équations 1.1 Introduction

Externat des Enfants Nantais
Jean-Marc BERROU
TP7 | Résolution approchée d’équations
1.1 Introduction
ca
l
cu
l
app
r
oché de
l
a
r
ac
i
ne d
’
une équa
ti
on
du
ty
pe
O
n
utilisera différentes méthodes dont certaines résulteront d’une étude mathématique
(suites récurrentes, encadrements, dichotomie).
Exercice 1

Jean-Marc BERROU
1.2 Méthode de dichotomie
Principe
I
n
iti
a
li
sa
ti
on
:
0
0
0
It
é
r
a
ti
on
:
+
2
+1 +1
+1 +1
A
rr
ê
t :
Justication de la convergence
+1 +1 +
2 +1
+1
→∞
→∞ 00
0
0 0
Mise en œuvre
TP

Externat des Enfants Nantais
Jean-Marc BERROU
e=input("précision : ")
a=valeurinferieure
b=valeursuperieure
while b-a>e
c=(a+b)/2
if TP(a)*TP(c)>0then
a=c
else
b=c
end
end
disp(a,"la solution est environ ")
Exercice 2
//
tp6
32
Si vous avez terminé en avance...
Démon
tr
ez que
l’
équa
ti
on adme
t
une un
i
que so
l
u
ti
on dans
1.3 Approximation par une suite itérative
continue 0
0
+1
si
E
x
e
r
c
i
ce
3
1

Jean-Marc BERROU
E
x
e
r
c
i
ce
4
2
0
suite
n
phi
suite
phi
approx
p
suitephi
1.4 Complément : Méthode de Newton
f
1.5 Méthode de la sécante
Principe
2
′

Externat des Enfants Nantais
Jean-Marc BERROU
1.6 Exercices
Exercice 5 Une résolution par dichotomie
23
2
−4
On pourra écrire dans un premier temps une fonction qui calcule pour une entrée .
Exercice 6 Une résolution par itération
0 +1
−6
Exercice 7 Une équation, deux méthodes
2−
1
2
On rappelle que
−6
0 +1
−6
 6
6
 7
7
 8
8
1
/
8
100%