La méthode de Newton : Principe de la méthode

Algorithmique : La méthode de Newton :
Principe de la méthode :
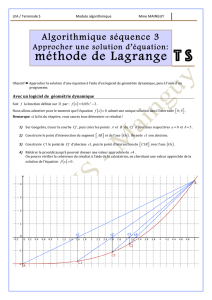
On cherche à déterminer une solution approchée d'une équation du type f(x) = 0 (E)
On suppose que la fonction f est dérivable sur un intervalle I contenant une solution de (E) et que l'on connait sa
dérivée f '. On choisit un point de départ x0 dont on suppose qu'il « n'est pas trop loin de cette solution ». On
remplace alors la fonction f par la fonction g0 représentant la tangente à la courbe de f au point d'abscisse x0. On
résout alors l'équation : g0(x) = 0. On appelle x1 la solution de cette équation.
On itère ensuite la méthode en partant de x1. et ainsi de suite... On obtient alors une suite de réels qui semblent
converger très rapidement vers la solution de l'équation f(x) = 0.

1) Déterminer la valeur de x1 en fonction de x0, puis celle de x2 en fonction de celle de x1.
2) En déduire une condition sur f '(x0) pour que x1 existe et une condition sur f '(x1) pour que x2 existe.
Traduire cette condition graphiquement.
3) Trouver graphiquement un exemple pour lequel la méthode de Newton de donne pas une suite de réels
se rapprochant de la solution de l'équation de f(x) = 0 (On dit alors que la méthode ne converge pas.
Mise en place d'un algorithme :
1) Ecrire en langage naturel un algorithme permettant de calculer les premiers nombres de la méthode de
Newton pour une fonction donnée.
Un problème apparaît alors rapidement : Comment décider l'arrêter les calculs ? Dans cet présentation de la
méthode, on choisira d'arrêter les calculs dès que f(xi) est inférieur à un nombre arbitraire donné, 10-5 par
exemple.
2) Modifier l'algorithme précédent afin d'y inclure le test d'arrêt proposé ci-dessus.
3) Implémenter cet algorithme dans la calculatrice et le tester pour f définie sur
ℝ
par f(x) = x2 -2 et
x0 = 2. De quel nombre la méthode de Newton permet-elle ainsi d'obtenir une valeur approchée?
4) Tester maintenant cet algorithme pour la fonction f définie sur
ℝ
par f(x) = x1/3 et x0 = 1. Que se
passe-t-il?
Le second problème que l'on peut rencontrer est que la méthode de Newton peut ne pas converger. Il faut donc
prévoir une sortie de boucle pour éviter que le programme ne tourne indéfiniment.
5) Proposer une modification du test d'arrêt précédent pour être sûr que la méthode ne dépasse pas 500
itérations et faire alors afficher un message d'erreur du type : « nombre d'itérations maximale dépassée, il se
peut que la méthode ne converge pas... »