Intégrales et primitives
Terminale S
Intégrales et
primitives
Décembre 2013
Table des
matières
Objectifs 5
Introduction 7
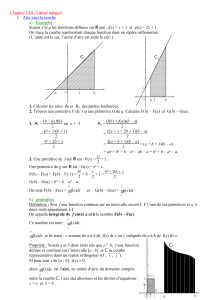
I - Intégrale d'une fonction continue positive 9
9
10
!"!11
#$%!!14
1. Sur calculatrice TI...........................................................................................................14
2. Sur calculatrice Casio.......................................................................................................15
&
'(%!!!$$"!)!!))!16
*$!!%"!)!!17
+,!!!%19
-!%!!19
II - Notion de primitive 21
#)!!21
.$!%$21
,/)!!!!$0123$%$22
#4!"!)!!$!%22
III - Calcul de primitives 25
'$)56)76825
'$)!!$$$26
%$29
#.$$!30
IV - Propriétés de l'intégrale 31
!"!)!!!!$!!31
!!32
!$$32
#!"!34
'$38
*"!!43
V - Valeur moyenne d'une fonction 45
"%%45
9!!46
."%%!49
VI - Tester ses connaissances 51
Solution des exercices 55
Contenus annexes 65
:
Objectifs
#!$%;!$2!$$!!$$!$
!"!"!)!!!!
!!
!!%$
%$
'%$"!
9!!"!)!!$!!
<
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
1
/
68
100%
