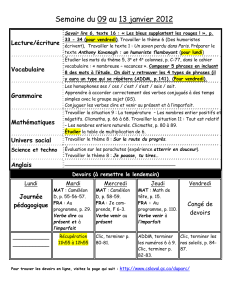
Pour réussir en Prépa HEC (voie économique)

Pour r´eussir en Pr´epa HEC
(voie ´economique)
A. RIDARD

2

Table des mati`eres
Pr´eface................................ 7
I Espaces vectoriels. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
1. Pour montrer qu’un sous ensemble est un sev . . . . . . . . . . . . . . . . . . . . . . . . . 9
2. Pour montrer qu’un ensemble est un ev . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
3. Pour montrer que deux ev sont ´egaux . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
a. Endimensionquelconque ................................ 9
b. Endimensionfinie .................................... 9
4. Pour d´eterminer la dimension d’un ev . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
5. Pour montrer que E=F⊕G.................................. 9
a. Endimensionquelconque ................................ 9
b. Endimensionfinie .................................... 9
6. Pour montrer qu’une famille est libre . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
7. Pour montrer qu’une famille est li´ee . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
8. Pour montrer qu’une famille est g´en´eratrice . . . . . . . . . . . . . . . . . . . . . . . . . . 10
9. Pour montrer qu’une famille est une base . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
a. Endimensionquelconque ................................ 10
b. Endimensionfinieconnue................................ 10
II Applications lin´eaires . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
1. Pour montrer que festlin´eaire................................. 11
2. Pour montrer que f∈ L(E, F ) ................................. 11
3. Pour d´efinir une application lin´eaire . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
4. Pour d´eterminer le rang d’une application lin´eaire . . . . . . . . . . . . . . . . . . . . . . 11
5. Pour montrer qu’une application lin´eaire est injective . . . . . . . . . . . . . . . . . . . . . 11
a. Endimensionquelconque ................................ 11
b. Endimensionfinie .................................... 11
6. Pour montrer qu’une application lin´eaire est surjective . . . . . . . . . . . . . . . . . . . . 12
a. Endimensionquelconque ................................ 12
b. Endimensionfinie .................................... 12
7. Pour montrer qu’une application lin´eaire est bijective . . . . . . . . . . . . . . . . . . . . . 12
a. Endimensionquelconque ................................ 12
b. Endimensionfinie .................................... 12
8. Pour montrer que hestunehomoth´etie ............................ 12
9. Pour montrer que pestunprojecteur ............................. 12
10. Pour montrer que sestunesym´etrie.............................. 12
III Matrices d’endomorphismes . . . . . . . . . . . . . . . . . . . . . . . . . 13
1. Pour d´eterminer MB(u) o`u B= (ei)1≤i≤n........................... 13
2. Pour d´eterminer MB(u+λv) .................................. 13
3. Pour d´eterminer MB(uov).................................... 13
4. Pour d´eterminer les coordonn´ees de u(x)............................ 13
5. Pourchangerdebase....................................... 13
a. Au niveau de la matrice d’un endomorphisme . . . . . . . . . . . . . . . . . . . . . 13
b. Au niveau des coordonn´ees d’un vecteur . . . . . . . . . . . . . . . . . . . . . . . . 14
6. Pour calculer une puissance de matrice . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
7. Pour montrer qu’une matrice A∈ Mnestinversible ..................... 14
8. Pour calculer l’inverse d’une matrice inversible . . . . . . . . . . . . . . . . . . . . . . . . 14
3

IV Diagonalisation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
1. Pour d´eterminer les ´el´ements propres d’un endomorphisme . . . . . . . . . . . . . . . . . . 15
2. Pour d´eterminer les ´el´ements propres d’une matrice . . . . . . . . . . . . . . . . . . . . . . 15
3. Pour montrer qu’une matrice est diagonalisable . . . . . . . . . . . . . . . . . . . . . . . . 15
a. Quand la matrice est r´eelle sym´etrique . . . . . . . . . . . . . . . . . . . . . . . . . 15
b. Quand la matrice de taille nanvaleurs propres distinctes deux `a deux . . . . . . 15
c. Eng´en´eral ........................................ 15
4. Pour diagonaliser une matrice diagonalisable . . . . . . . . . . . . . . . . . . . . . . . . . 16
V Suites................................. 17
1. Pour ´etudier la monotonie d’une suite . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
a. Quand unestunesomme ................................ 17
b. Quand unestunproduit ................................ 17
c. Quand un=f(n)..................................... 17
2. Pour ´etudier la convergence d’une suite . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
3. Pour ´etudier une suite r´ecurrente . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
a. Quandelleestclassique ................................. 18
b. Quand ”un+1 =f(un)” ................................. 18
VI S´eries................................. 19
1. Pour montrer qu’une s´erie diverge (grossi`erement) . . . . . . . . . . . . . . . . . . . . . . 19
2. Pour ´etudier la convergence d’une s´erie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
a. Atermespositifs..................................... 19
b. Atermesquelconques .................................. 19
3. Pour d´eterminer la somme d’une s´erie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
a. Quand Snsecalcule ................................... 20
b. Quand Snnesecalculepas ............................... 20
4. Formulaire............................................. 20
VII Fonctions num´eriques r´eelles . . . . . . . . . . . . . . . . . . . . . . . . . 21
1. Pour´etudierunefonction .................................... 21
2. Pour prolonger une fonction par continuit´e en un point . . . . . . . . . . . . . . . . . . . . 21
3. Pour ´etudier la d´erivabilit´e en un point . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
4. Pour lever une ind´etermination . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
a. De la forme 0
0en un r´eel a................................ 22
b. De la forme +∞−∞ .................................. 22
c. De la forme ∞
∞...................................... 22
d. De la forme 1∞...................................... 22
5. Pour montrer une in´egalit´e . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
VIII Formules de Taylor . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
1. Pour obtenir le comportement d’une fonction . . . . . . . . . . . . . . . . . . . . . . . . . 23
a. Globalement ....................................... 23
b. Localement (´etude d’une branche infinie par exemple) . . . . . . . . . . . . . . . . 23
2. Pourcalculerdesdl ....................................... 23
3. Pourr´eussirlesdl ........................................ 23
4. Pour lever une ind´etermination dans un calcul de limite . . . . . . . . . . . . . . . . . . . 23
5. Formulaire............................................. 24
a. Dlen0 .......................................... 24
b. Equivalentsen0 ..................................... 24
IX Int´egrales propres. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
1. Pourcalculeruneprimitive ................................... 25
a. D’unefonctionusuelle.................................. 25
b. D’une fonction rationnelle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
2. Pourcalculeruneint´egrale.................................... 25
3. Pourborneruneint´egrale .................................... 26
4. Pour ´etablir une in´egalit´e entre deux int´egrales . . . . . . . . . . . . . . . . . . . . . . . . 26
5. Pour montrer qu’une fonction continue est nulle . . . . . . . . . . . . . . . . . . . . . . . . 26
6. Pour transformer une int´egrale en une int´egrale ”exploitable” . . . . . . . . . . . . . . . . 26
4

7. Pour montrer qu’une suite d´efinie par un=Zb
a
fn(t)dt converge .............. 26
8. Pour d´eriver une fonction d´efinie par G(x) = Zv(x)
u(x)
f(t)dt .................. 26
X Int´egrales impropres. . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
1. Pour ´etudier la convergence d’une int´egrale une fois impropre . . . . . . . . . . . . . . . . 27
a. Quand fest prolongeable par continuit´e sur [a, b]................... 27
b. Quand festprimitivable ................................ 27
c. Quand festpositive................................... 27
d. Quand fn’est pas de signe constant . . . . . . . . . . . . . . . . . . . . . . . . . . 28
2. Pour ´etudier la convergence d’une int´egrale plusieurs fois impropre . . . . . . . . . . . . . 28
3. Pour calculer avec des int´egrales impropres . . . . . . . . . . . . . . . . . . . . . . . . . . 28
XI Fonctions num´eriques de deux variables. . . . . . . . . . . . . . . . . . . . . 29
1. Pour calculer les d´eriv´ees partielles d’ordre 1 de f...................... 29
2. Pour montrer que fest de classe C1.............................. 29
3. Pour obtenir le DL de fen (a, b)`al’ordre1.......................... 29
4. Pour calculer les d´eriv´ees partielles d’ordre 2 de f...................... 29
5. Pour montrer que fest de classe C2.............................. 29
6. Pour obtenir le DL de fen (a, b)`al’ordre2.......................... 29
7. Pour d´eterminer les extremums de f.............................. 30
XII D´enombrement et probabilit´es classiques . . . . . . . . . . . . . . . . . . . . 31
1. Pourd´enombrer.......................................... 31
a. Avecordreetr´ep´etition ................................. 31
b. Avec ordre et sans r´ep´etition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
c. Sansordrenir´ep´etition ................................. 31
d. Sans ordre et avec r´ep´etition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
2. Pour calculer P(A∪B) ..................................... 31
a. Quand Aet Bsontincompatibles ........................... 31
b. Quand Aet Bne sont pas incompatibles . . . . . . . . . . . . . . . . . . . . . . . 32
3. Pour calculer P(A∩B) ..................................... 32
a. Quand Aet Bsontind´ependants............................ 32
b. Quand Aet Bne sont pas ind´ependants . . . . . . . . . . . . . . . . . . . . . . . . 32
4. Pour calculer P(A)........................................ 32
a. Sous l’hypoth`ese d’´equiprobabilit´e . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
b. Quand P(A) est plus facile `a calculer . . . . . . . . . . . . . . . . . . . . . . . . . 32
c. Quand Aest li´e `a un ´ev´enement B........................... 32
5. Pour calculer P(B|A) `a partir de P(A|B) ........................... 33
6. Pour montrer que des ´ev´enements sont mutuellement ind´ependants . . . . . . . . . . . . . 33
XIII Va discr`etes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
1. Pour ´etudier le nombre de succ`es au terme de nr´ep´etitions ind´ependantes d’une exp´erience
`adeuxissuespossibles...................................... 35
2. Pour ´etudier le nombre d’individus `a caract`ere donn´e au terme d’un tirage simultan´e (ou
successif mais sans remise) de nindividus parmi N...................... 35
3. Pour ´etudier l’attente du premier succ`es au cours de r´ep´etitions ind´ependantes d’une
exp´erience `a deux issues possibles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
4. Pour d´eterminer la loi de X................................... 35
5. Pour r´esoudre les probl`emes de couples . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
6. Pour ´etudier X+You XY ................................... 36
7. Pour d´eterminer l’esp´erance de . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
a. X............................................. 36
b. f(X)............................................ 37
c. aX +bY ......................................... 37
d. XY ............................................ 37
8. Pour d´eterminer la variance de . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
a. X............................................. 37
b. aX +b........................................... 37
5