CHAPITRE 17 : Angles inscrits, angles au centre. I. Définitions. Dans

3
ème
1
Chapitre 17 : angles au centre, angles inscrits.
CHAPITRE 17 :
Angles inscrits, angles au centre.
I. Définitions.
Dans un cercle :
 un angle intercepte un arc de cercle AB si ses côtés sont sécants avec
le cercle au point A et B.
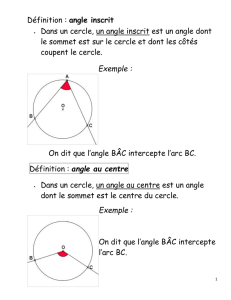
 un angle inscrit est un angle dont le sommet est un point du cercle et
les côtés sont sécants avec le cercle.
 un angle au centre est un angle dont le sommet est le centre du cercle.
Exemples :
• ACB est un angle inscrit, son sommet C est sur le cercle et ses côtés
[CA) et [CB) coupent le cercle en A et B. Cet angle intercepte l’arc AB.
• DOE est un angle au centre, son sommet O est le centre du cercle. Cet
angle intercepte l’arc DE .
Remarque :
Avec deux points sur un cercle, on définit deux arcs de cercle et avec 3 points on définit deux angles, l’angle
saillant et l’angle rentrant. On dit que l’angle intercepte l’arc qui ne contient pas son sommet.
Exemples :
L’angle saillant AÔB et l’angle inscrit ACB intercepte
le même arc AB.
L’angle rentrant AOB et l’angle inscrit ACB intercepte
le même arc AB.
II. Propriétés.
 Dans un cercle, si un angle au centre et un angle inscrit interceptent le même arc alors la mesure de l’angle
au centre est le double de la mesure de l’angle inscrit.
 Dans un cercle, si deux angles inscrits intercepte le même arc alors ils ont la même mesure.

3
ème
2
Chapitre 17 : angles au centre, angles inscrits.
Exemples :
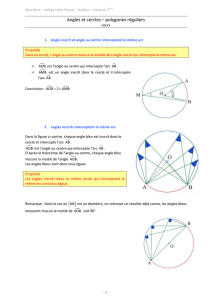
1)
L’angle saillant AÔB et l’angle inscrit ACB intercepte
le même arc AB.
Donc AÔB = 2 × ACB
L’angle rentrant AOB et l’angle inscrit ACB intercepte
le même arc AB.
Donc AOB = 2 × ACB
2)
Les angles inscrits ACB et ADB interceptent le même arc AB, donc
ACB = ADB
Remarque :
Une conséquence de ces propriétés est la propriété du triangle rectangle :
Si un triangle est inscrit dans un cercle ayant pour diamètre un côté de ce
triangle alors ce triangle est rectangle.
L’angle saillant AÔB et l’angle
inscrit ACB intercepte le même
arc AB. Donc AÔB = 2 × ACB.
Et on sait que l’angle au centre AÔB est plat donc AÔB = 180°
donc ACB = 1
2 × AÔC = 180 2 = 90°