Terminale S CORRECTION du DS 3 du 21 novembre (2 h)

Terminale S CORRECTION du DS 3 du 21 novembre (2 h)
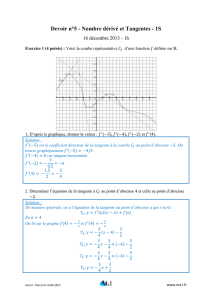
Exercice 1 (9 points)
 est la fonction définie sur  par  
1) La fonction  est une fonction polynôme, elle est donc dérivable sur IR.
De plus, pour tout nombre réel x, réel  
Ce trinôme a un discriminant négatif, il est donc du même signe que son coefficient dominant     .
On en déduit que la fonction dérivée de  est strictement positive, ce qui prouve que
la fonction  est strictement croissante sur IR.
2)  est continue (car dérivable) et strictement croissante sur IR, de plus  et   .
Il résulte du corollaire du théorème des valeurs intermédiaires que
l'équation   admet une unique solution  sur IR et que   
3) étant strictement croissante, si    alors   , si   alors   ,
si    alors   .
Partie B
1)
a b b-a (a+b)/2 g((a+b)/2) à 0,001 près
Initialisation -1 0 1 -0,5 -0,875
Boucle
-0,5 0 0,5 -0,25 0,172
-0,5 -0,25 0,25 -0,375 -0,318
-0,375 -0,25 0,125 b-a étant inférieur à 0,15, afficher a et
b
Les valeurs affichées par cet algorithme sont les bornes du premier intervalle d'amplitude inférieure à 0,15
contenant , obtenu par la méthode de dichotomie. Les résultats affichés sont -0,375 et -0,25.
2) a) Tant que   faire  prend la valeur .
b) L’algorithme 2 affiche une valeur approchée de à 0,1 près par défaut. Le résultat affiché est -0,3.
3) On obtient à l'aide de la calculatrice -0,296    -0,295.
Partie C
1) La fonction  définie sur IR par   
!"#
est la somme d'une fonction affine et d'une fonction
rationnelle dont le dénominateur ne s'annule pas sur IR, elle est donc définie et dérivable sur IR.
Pour tout nombre réel x, $ %
 !"#&
'
 !"#&
 !"#&"'
 !"#&
.
nous avons d'une part ! (  
'
(
et d'autre part    
' '
(
Ce qui permet d'affirmer que pour tout nombre réel x, )$
"
!"*
.

2) La fonction $ est une fonction rationnelle dont le dénominateur est strictement positif, son signe est donc
celui de son numérateur, d'où le tableau de variation de , en tenant compte des résultats de la partie A et du
fait qu'il a été démontré que    .
– ∞ –1  +∞
– 0 + +
– – 0
+ 0 – 0 +
?
–2 ?
Exercice 2 (3 points)
On a tracé ci-dessous les courbes représentatives des fonction  et  définies sur  par +!    
et  
#
'
!   
#
'
1) Que peut-on conjecturer que les tangentes au point d’abscisse 1 à ,
)
et à , sont confondues
2) L’équation de la tangente au point d’abscisse 1 à -
.
est
/  
0
L’équation de la tangente au point d’abscisse 1 à -
1
est
/  
0
Ces tangentes sont confondues si et seulement si   et 
0 0
.
On a immédiatement   
 et  sont dérivables sur  (pour  car !       pour  dans  : à vérifier) et pour tout réel $:
0
 2#
+ !2 "#
et 
0
#
On a donc 
0 0
#
Les tangentes au point d’abscisse 1 à ,
)
et à , sont bien confondues.

Exercice 3 (4 points)
1 – a) Soit une fonction définie et dérivable sur IR telle que    et  .
On définit une fonction h sur IR en posant h(x)=f(x)×f(−x) = u(x)×v(x).
Cette fonction est un produit de deux fonctions définies sur IR, elle est donc définie sur IR.
La fonction u est dérivable par hypothèse, et la fonction v est de la forme v(x) = f(ax+b) où a et b sont des
constantes réelles (a=-1 et b=0), v est donc dérivable sur IR, et pour tout réel x, v'(x) = af '(ax+b) = -f '(-x).
La fonction h est donc dérivable sur IR et pour tout réel x,
h'(x) = u'(x)×v(x) + u(x)×v'(x) =f '(x)×f(−x) + f(x)×(-f'(−x)) = 0 (puisque   )
ceci prouve que la fonction h est constante sur IR.
Or h(0) = f(0)×f(−0) = 1, donc pour tout réel x, f(x)×f(−x) =1
b) On suppose qu'il existe deux fonctions,  et , dérivables sur IR et vérifiant :    et  . On définit
une fonction k sur IR en posant : k(x)=f(−x)×g(x).
Cette fonction est un produit de deux fonctions dérivables sur IR, (voir la question a) elle est donc dérivable
sur IR. De plus, pour tout nombre réel x,
k'(x) = -f '(-x)×g(x) + f(-x)×g '(x) =-f(-x)×g(x) + f(-x)×g(x) (puisque   et   )
ainsi, pour tout nombre réel x, k'(x) = 0, ce qui prouve que la fonction k est constante sur IR .
De plus k(0) = f(-0)×g(0) = 1 donc pour tout nombre réel x, f(−x)×g(x) = 1
En multipliant les deux membres de cette égalité par f(x), on obtient
pour tout nombre réel x, f(x)×f(-x)×g(x) = f(x) et en utilisant le résultats de la question a) : g(x) = f(x),
ce qui prouve l'égalité des fonctions f et g, puis l'unicité de la solution du problème.
2 – Application : pour tout nombre réel x,
3456 75  89
9
2
:
89
9
2
:
9
9
2
(9
9
2
(
d'où 3;<6
*
=<
*
>*"*>>?">?*
@
>*2*>>?">?*
@
@>>?
@
Exercice 4 (4 points)
est un cercle de centre O et de rayon 3 m.
Sur la perpendiculaire en O au plan du cercle, on place une source lumineuse S.
On souhaite savoir à quelle hauteur , exprimée en m, placer S pour que
l’éclairement du cercle soit maximal.
Une loi physique nous assure que l’éclairement du cercle est proportionnel à
 &"A+ !"A
On a entré dans un logiciel de calcul formel les commandes suivantes :

1)  est dérivable sur $$B car c’est le quotient de deux fonctions dérivables dont le dénominateur ne
s’annule pas sur $$B.
Xcas nous donne 
0
2 &"A+ !"A
 &"AC
pour  dans $$B.
Pour  dans $$B$, +!D   et  D   ,
donc 
0
 et 
D ont le même signe sur $$B.
D   E !  D
E     
F$$$$$GHI$  
D’où le tableau :
2) Pour que l’éclairement soit maximal, il faut donc que
JK  L
F*$M N **$M
3) On veut ici calculer 
0
.
On a  
O
P
avec Q  et R  D+!D
Donc Q
0
  et R  S avec  
D et S+!D
donc 
0
  et S
0
+ !"A
On a R
0 0
SS
Donc R
0
 +!D
 &"A
+ !"A
 +!D
On a 
0
OTP2OP0
P!
Donc )
0
3*"U6+*"U2%L+!"U
*"UL
2**"U+!"U
*"UL