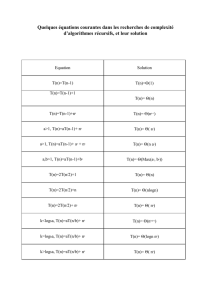
Formules explicites pour suites définies récursivement

Schweizer Mathematik-Olympiade
Formules explicites pour suites définies
récursivement
Aktualisiert: 26. Juni 2014
Dans ce script on va vous expliquer comment trouver des formules explicites à partir de
suites définies récursivement. Pour commencer, considérons une suite réelle (ou complexe)
a0, a1, . . . donnée par les valeurs a0, . . . , an−1et par l’équation de récurrence
ak+n+cn−1ak+n−1+. . . +c1ak+1 +c0ak= 0 ∀k≥0,(1)
avec les cides constantes. Il est facile de voir que le reste de la suite est ainsi entièrement
déterminée. On cherche une forme explicite pour les termes de la suite et pour cela on
commence par poser an=λn. En introduisant cette expression dans (1), on obtient
chp(λ) = λn+cn−1λn−1+. . . +c1λ+c0= 0
qui ne dépend plus de k. On appelle le côté gauche de l’équation le polynôme carac-
téristique de l’équation de récurrence. Par conséquent λdoit être un zéro du polynôme
caractéristique. Ces zéros nous donnent ensuite les solution fondamentales que nous allons
maintenant décrire. Quand le polynôme caractéristique a des zéros multiples, quelques
difficultés apparaissent. Sans prouver les affirmations suivantes (ce qui serait assez diffi-
cile), voici la description de la façon de procéder.
Soient λ1, . . . , λrles zéros distincts de chp(λ)avec leurs multiplicités respectives m1, . . . , mr≥
1. Considérons maintenant pour tout 1≤i≤rles misolutions fondamentales distinctes
Fi,j (k) = kj·λk
i,0≤j≤mi−1.
La suite akest ainsi une combinaison linéaire uniquement déterminée de ces solutions
fondamentales. Nous avons en effet la proposition suivante:
Satz 0.1. Il existe des constantes (complexes) uniquement déterminées Ci,j telles que
ak=
r
X
i=1
mi−1
X
j=0
Ci,j ·Fi,j (k),∀k≥0.
On trouve les coefficients Ci,j en introduisant k= 0,1, . . . , n −1dans l’équation ci-haut
et en résolvant le système de néquations en nvariables Ci,j qui en résulte.
La proposition décrit bien sûr le cas le plus compliqué que l’on ne rencontre pratiquement
jamais. Voici maintenant quelques exemples.

Beispiel 1. La suite de Fibonacci est définie par a0= 0, a1= 1 et la formule de récur-
rence an+2 =an+1 +anpour n≥0. Trouver une formule explicite pour an.
Solution. Le polynôme caractéristique est chp(λ) = λ2−λ−1. Les deux zéros du poly-
nôme sont λ1,2= (1 ±√5)/2et ils sont les deux de mulltiplicité 1. Les deux solutions
fondamentales sont par conséquent F1(n) = ((1 + √5)/2)net F2(n) = ((1 −√5)/2)n.
Nous obtenons ainsi une formule de la forme
an=C1 1 + √5
2!n
+C2 1−√5
2!n
.
Les constantes C1,2peuvent être déterminées à l’aide des valeurs a0= 0 et a1= 1. Le
système d’équations suivant doit être satisfait:
0 = C1+C2,
1 = C1 1 + √5
2!+C2 1−√5 2!.
Il s’ensuit que C1= 1/√5et C2=−1/√5, ce qui nous amène à la formule de Binet bien
connue:
an=1
√5" 1 + √5
2!n
− 1−√5
2!n#.
Beispiel 2. La suite de Lucas ressemble à celle de Fibonacci, elle est définie par b1=
1, b2= 3 et la formule de récurrence bn+2 =bn+1 +bnpour n≥1. Trouver une formule
explicite pour cette suite.
Solution. Pour simplifier les calculs et commencer la suite à b0, posons b0= 2 (ce qui est
consistant par rapport à l’équation de récurrence). La suite de Lucas et celle de Fibonacci
ont la même équation de récurrence et par conséquent les mêmes solutions fondamentales.
Il n’y a que les constantes qui changent. Le nouveau système d’équations est
2 = C1+C2,
1 = C1 1 + √5
2!+C2 1−√5 2!.
Les solutions sont C1=C2= 1, ce qui entraîne
bn= 1 + √5
2!n
+ 1−√5
2!n
.
2

On peut obtenir beaucoup de résultats spectaculaires à partir des expressions explicites
que l’on vient de trouver. Un exemple plutôt anodin est la formule de limite bien connue
pour la suite de Fibonacci
lim
n→∞
an
an−1
=1 + √5
2.
Le terme de droite s’appelle le nombre d’or. Il apparaît de façon très naturelle dans les
problèmes d’emplacement optimal. Cela explique peut-être pourquoi la suite de Fibonacci
est aussi omniprésente dans la nature (comptez par exemple le nombre de spirales d’une
pomme de pin ou les spirales dans une fleur de tournesol).
Dans l’exemple suivant, le polynôme caractéristique possède des zéros multiples:
Beispiel 3. Deux suites anet bn,n≥0, satisfont les équations suivantes:
bn=an+an−1+an−2
bn+bn−2= 4(an−1+an−3).
De plus soient a0=a1= 1 et b2=b3= 4. Trouver une formule explicite pour an.
Solution. En introduisant la première équation dans la deuxième, nous obtenons an−
2an−1+ 2an−2−2an−3+an−4= 0 pour tout n≥4. Le polynôme caractéristique chp(λ) =
λ4−2λ3+ 2λ2−2λ+ 1 = (λ2+ 1)(λ−1)2admet le zéro double λ= 1 et les deux zéros
complexes conjugués λ=±i. D’après la proposition 1, il existe des constantes A, B, C, D
telles que
an=A+B·n+C·in+D·(−i)n.
En partant des valeurs initiales données et de la première équation en haut, nous obtenons
facilement a2= 2 et a3= 1. Cela nous donne le système d’équations
1 = A+C+D
1 = A+B+iC −iD
2 = A+ 2B−C−D
1 = A+ 3B−iC +iD
avec les solutions A= 2,B=−1/2,C= (−2 + i)/4et D= (−2−i)/4. En remplaçant
ces valeurs dans la formule ci-dessus, on obtient
an=
1−n/2n≡0(mod 4)
3/2−n/2n≡1(mod 4)
3−n/2n≡2(mod 4)
5/2−n/2n≡3(mod 4)
Cet exemple met en lumière le fait que même si la suite anest clairement réelle, il se peut
qu’il y ait des nombres complexes dans la formule explicite. Toutefois si l’équation de
3

récurrence n’a que des coefficient réels, alors les zéros complexes du polynôme caractéris-
tique apparaissent toujours accompagnés de leurs conjugués, ce qui est par conséquent
le cas pour les termes complexes de la formule explicite également. Si les valeurs initiales
sont réelles, alors les coefficients correspondants sont également conjugués et en effectuant
les transformations adéquates on arrive à faire disparaître les parties imaginaires de la
formule. Il ne reste que des nombres réels. Ceci peut être démontré, mais pour vous il
suffit de le savoir. Dans la plupart des applications il devient vite clair comment certains
termes se simplifient.
Voici maintenant une véritable application.
Beispiel 4. Trouver toutes les fonctions f:R>0→R>0telles que pour tout x > 0,
f(f(x)) + f(x) = 2x.
Solution. Soit a > 0un nombre arbitraire. Définissons une suite anpar a0=aet an+1 =
f(an). Nous avons alors, par hypothèse, l’équation de récurrence an+2 +an+1 = 2an. Le
polynôme caractéristique admet les zéros 1 et −2, il existe donc des constantes Aet B
avec
an=A·1n+B·(−2)n.
Comme fne prend que des valeurs positives, tous les termes ande la suite doivent être
positifs. Si on avait B6= 0, alors il y aurait des ntrès grands pour lesquels le côté droit
de la formule serait négative, contradiction. Par conséquent B= 0 et a0=A=a1, donc
f(a) = a. Comme aétait arbitraire, on a montré que
f(x) = x∀x∈R>0.
Une représentation explicite peut donc souvent être utile. L’opération inverse est ce-
pendant tout aussi importante. Il y a souvent des termes qui font penser à certaines
formules explicites de suites définies récursivement. A l’aide de l’équation de récurrence,
nous pouvons parfois démontrer des assertions concernant la divisibilité et autres sujets
semblables. En voici maintenant un exemple.
Beispiel 5. Existe-t-il un nombre naturel impair ntel que b(2 + √5)ncsoit divisible par
99?
Solution. L’expression donnée sous cette forme ne convient pas du tout à des consi-
dérations de divisibilité. Pour des raisons de symétrie, on pourrait considérer à la place
l’expression
an= (2 + √5)n+ (2 −√5)n.(2)
Nous allons montrer que c’est un nombre entier. De là et de l’estimation 0>2−√5>−1,
il s’ensuivra directement que pour un nimpair, nous avons en effet que b(2 + √5)nc=
4

(2 + √5)n+ (2 −√5)n. L’expression (2) fait penser à la formule explicite d’une suite
définie récursivement. Nous allons maintenant reconstruire cette formule de récurrence. Le
polynôme caractéristique doit admettre les deux zéros 2±√5, nous avons donc chp(λ) =
λ2−4λ−1. La formule de récurrence est par conséquent
an+2 = 4an+1 +an.
Nous avons de plus a0= 2 et a1= 4. Par conséquent anest entier pour tout n≥0. Nous
devons encore décider si anpeut être divisible par 99. Pour cela nous allons considérer
la suite modulo 9 et modulo 11. Un calcul rapide nous donne les périodes minimales
2,4,0,4,7,5,0,5modulo 9 et 2,4,7,10,3,0,3,1,7,7modulo 11. Il s’ensuit que 9|an⇔
n≡2,6(mod 8) et 11 |an⇔n≡5(mod 10). Ces deux congruences ne sont jamais
satisfaites en même temps, par conséquent ann’est jamais divisible par 99.
Exercices
1. Soit Fnla suite de Fibonacci et Lnla suite de Lucas comme définies précédemment.
Montrer que n
Y
k=0
L2k=F2n+1 .
2. (OMI 79) Soient Aet Edeux sommets opposés d’un octogone régulier. Une gre-
nouille part de Aet saute de chaque sommet sauf Eà un sommet voisin. Si elle
arrive en E, elle arrête de sauter. Soit anle nombre de chemins différents de Aen
Ede longueur n. Montrer que a2n−1= 0 et
a2n=(2 + √2)n−1
√2−(2 −√2)n−1 √2.
3. Trouver toutes les fonctions f:R>0→R>0telles que pour tout x > 0,
f(f(f(x))) + f(f(x)) + f(x) = 3x.
Généraliser.
4. (OMI de substitution 80) Déterminer le premier chiffre avant et après la virgule
dans la représentation décimale de
√2 + √31980
.
5. Déterminer la plus grande puissance de deux qui divise
j(1 + √3)nk.
6. (Shortlist 88) Soit ble plus grand zéro réel du polynôme x3−3x2+ 1. Montrer que
bb1788cet bb1988csont les deux divisibles par 17.
5