dst18classe23date31012017

DST 18 seconde3 31012017
vérification du sérieux
1/ Soient A(3,8); B(8,-2); C(5,4).
1.1/ Quelles sont les coordonnées du vecteur  +  ?
(8-3, -2-8)
(5-3, 4-8) = (2,-4)
+  (7, -14)
1.2/ Soit D un point tel que
=  .
Trouver les coordonnées de D
On sait que    donc x(D) – 8 = 2 et y(D) – (-2)= -4
donc D(10,-6) CLG
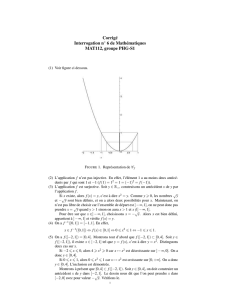
2/ Dessiner une fonction f définie sur [-8,8] qui est croissante sur [-
8,1] et décroissante sur [1,8-3] et croissante sur [8-3,8] et qui
n'atteint pas son maximum en 1
3/ Soit f la fonction telle que pour tout nombre x : f(x) = x² + 8
3.1/ Trouver un antécédent de
(-5)²+8 par f
Cette question est un cadeau pur et dur : f( (-5) ) = (-5)² + 8
3.2/ Trouver deux nombres ayant la même image par f
f(5) = f(-5) ; f(1) = f(-1) ; etc…

4/ (E,P) est un univers probabilisé et on note P la fonction
probabilité. On suppose que
P(A  
) = 0.3 et P(A)= 0.7 et
P(B) = 0.6
Trouver P(A  B) et P(A B)