chap3 fonctions de reference

O
-2
4u v
f(v)
f(u)
Chapitre III :
FONCTIONS DE REFERENCE
I. RAPPEL : Fonction croissante, fonction décroissante
Définition :
f est une fonction définie sur un intervalle I.
• Dire que f est croissante sur I signifie que pour tous réels a et b de I : si a ≤ b alors f(a) ≤
f(b).
• Dire que f est décroissante sur I signifie que pour tous réels a et b de I : si a ≤ b alors
f(a) ≥ f(b).
Illustration : Les courbes C1 et C2 représentent respectivement des fonctions
f et g définies sur [-2 ; 4]. C1
• D’après l’allure de la courbe C1, pour tous réels u et v de [-2 ; 4], si u ≤ v
alors f(u) ≤ f(v). Donc f est croissante sur [-2 ; 4].
Graphiquement : « La courbe monte ».
• D’après l’allure de la courbe C2, pour tous réels u et v de [-2 ; 4], si u ≤ v
alors g(u) ≥ g(v). Donc g est décroissante sur [-2 ; 4]. C2
Graphiquement : « la courbe descend ».
II. Fonction « RACINE CARREE »
1. Définition
La fonction f définie sur [0 ; + ∞[ par f(x) = ! est appelée fonction racine carrée.
Remarques :
• 0!= 0.
• Pour tout réel x, ! ≥ 0.
2. Sens de variation
La fonction « racine carrée » est croissante sur [0 ; + ∞[.
x
0 +∞
f

Applications :
• Comparer les nombres suivants sans les calculer : 1,001!et 1,0007.
• Encadrer ! si 4 ≤ x ≤ 7.
3. Représentation graphique
Tableau de valeurs :
x
0
1
4
9
16
!
0
1
2
3
4
Graphique :
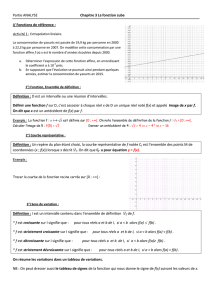
III. Fonction « CUBE »
1. Définition
La fonction f définie sur ℝ par f(x) = x3 est appelée fonction cube.
Remarques :
• Si x ≤ 0 alors x3 ≤ 0.
• Si x ≥ 0 alors x3 ≥ 0
2. Sens de variation
La fonction « cube » est croissante sur ℝ
x
-∞ +∞
f
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
2
3
4
0 1
1
x
y

Applications :
• Comparer les nombres suivants sans les calculer : ( 15)3 et 43.
• Encadrer x3 si -1 ≤ x ≤ 2.
3. Représentation graphique
Tableau de valeurs :
x
-2
-1,5
-1
0
1
1,5
2
x3
-8
3,375
-1
0
1
3,375
8
Graphique :
Remarques :
• La courbe est symétrique par rapport à l’origine du repère
• L’équation x3 = k (k étant une constante réelle) admet une unique solution que l’on calcule de la
manière suivante : x = !
! (appelée racine cubique de k).
Exemples : x3 = 343 x3 = -512 x3 = 25