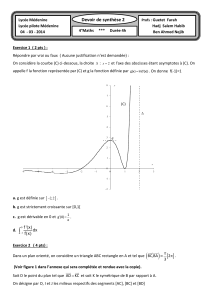
Bac blanc n°3 - j.galtier

Classe de Terminale S2 Mardi 24 mai 2005
Ultime devoir surveillé de mathématiques
Exercice 1 (bac S, Nouvelle Calédonie, mars 2005, 4 points)
L’exercice comporte 4 questions. Pour chaque question, on propose 3 affirmations. Pour
chacune d’elles, le candidat doit indiquer si elle est vraie ou fausse en rayant la case
correspondante. Aucune justification n’est demandée. Toute réponse ambiguë sera considérée
comme une absence de réponse. Chaque réponse exacte rapporte 0,25 point. Une bonification
de 0,25 point est ajoutée chaque fois qu’une question est traitée correctement en entier (c’est-
à-dire lorsque les réponses aux 3 affirmations sont exactes). 2 ou 3 réponses inexactes dans
une même question entraînent le retrait de 0,25 point. L’abstention n’est pas prise en compte,
c’est-à-dire ne rapporte ni ne retire aucun point. Si le total des points de l’exercice est négatif,
la note est ramenée à zéro.
Dans l’exercice, le plan complexe est rapporté au repère orthonormal
,,O u v
rr
.
1
Pour tout entier n non nul, pour
tout réel ,
n
i
e
est égal à :
ni
e
cos sin
nn
i
cos sinn i n
Faux
Vrai
Faux
Vrai
Faux
Vrai
2
La partie imaginaire du nombre
complexe z est égale à :
2
zz
2
zz
i
2
zz
Faux
Vrai
Faux
Vrai
Faux
Vrai
3
Soit z un complexe,
z x iy
(x
et y réels). Si z est un imaginaire
pur, alors
2
z
est égal à :
2
y
2
y
2
z
Faux
Vrai
Faux
Vrai
Faux
Vrai
4
A, B, C sont trois points d’affixes
respectives a, b, c telles que
3
ba i
ca
. Alors :
2BC AC
, 2 ,
2
AB AC k k
uuur uuur ¢
2
CA CB CA
uur uur
Faux
Vrai
Faux
Vrai
Faux
Vrai
Exercice 2 (Bac S, Nouvelle Calédonie, mars 2005, 5 points)
Une compagnie de transport désire optimiser les contrôles afin de limiter l’impact des fraudes
et les pertes occasionnées par cette pratique. Cette compagnie effectue une étude basée sur
deux trajets par jour pendant les vingt jours ouvrables d’un mois soit au total quarante trajets.
On admet que les contrôles sont indépendants les uns des autres et que la probabilité pour tout
voyageur d’être contrôlé est égale à p.
Le prix de chaque trajet est de dix euros, en cas de fraude l’amende est de cent euros. Claude
fraude systématiquement lors des quarante trajets soumis à cette étude.
Soit Xi la variable aléatoire qui prend la valeur 1 si Claude est contrôlé au i-ème trajet et la
valeur 0 sinon. Soit X la variable aléatoire définie par
1 2 40
...X X X X   
.

1. Montrer que X représente le nombre de fois où Claude est contrôlé, déterminer la loi de X.
2. Dans cette question on suppose que
1
20
p
.
a) Calculer l’espérance de X.
b) Calculer les probabilités
( 0), ( 1), ( 2)p X p X p X  
.
c) Calculer à 10-4 près la probabilité que Claude soit contrôlé au moins 3 fois.
3. Soit Z la variable aléatoire qui prend pour valeur le gain algébrique réalisé par le fraudeur
(par rapport à quelqu’un qui paierait tous ses trajets).
Justifier l’égalité
400 100ZX
puis calculer l’espérance de Z pour
1
5
p
.
4. On désire maintenant déterminer p afin que la probabilité que Claude subisse au moins
trois contrôles soit supérieure à 99%.
a) Démontrer que
38 2
( 2) (1 ) (741 38 1)p X p p p    
.
b) Soit f la fonction définie sur [0 ; 1] par
38 2
( ) (1 ) (741 38 1)f x x x x   
. Montrer que f
est strictement décroissante sur [0 ; 1] et qu’il existe un unique réel
0
x
appartenant à
[0 ; 1] tel que
0
( ) 0,01fx 
. Déterminer l’entier n tel que
01
100 100
nn
x
.
c) En déduire la valeur minimale qu’il faut attribuer à p pour que la probabilité que
Claude subisse au moins trois contrôles dans le mois soit supérieure ou égale à 99%
(on exprimera p en fonction de
0
x
).
Exercice 3 (Bac S, Inde, avril 2005, 5 points)
L’espace E est rapporté à un repère orthonormal
, , ,O i j k
r r r
.On considère les points A, B, C de
coordonnées respectives
(1; 0 ; 2)A
,
( 3; 4 ; 4)B
,
( 1;1;1)C
.
1. Montrer que A, B et C ne sont pas alignés. Soit
n
r
le vecteur de coordonnées
(3; 4; 2)n
r
.
Vérifier que
n
r
est orthogonal à
AB
uuur
et
AC
uuur
, en déduire une équation du plan (ABC).
2. Soient P1 et P2 les plans d’équations respectives
2 2 1 0x y z   
et
2 6 0x y z  
.
Montrer que P1 et P2 sont sécants suivant une droite D dont on donnera un système
d’équations paramétriques. La droite D et le plan (ABC) sont-ils sécants ou parallèles ?
3. Soit t un réel positif quelconque. On considère le barycentre G des points A, B, C affectés
des coefficients respectifs 1 ; 2 et t.
a) Justifier l’existence du point G pour tout réel positif t.
Soit I le barycentre des points A et B affectés des coefficients 1 et 2. Déterminer les
coordonnées du point I. Exprimer
IG
uur
en fonction de
IC
uur
.
b) Montrer que l’ensemble des points G lorsque t décrit
[0 ; [
est le segment [IC] privé
du point C. Pour quelle valeur de t G est-il le milieu de [IC] ?
Exercice 4 ( directement sorti du cerveau malade d’un professeur, 6 points)
Soit f la fonction définie sur
0;
par
1
( ) si 0, (0) 1
t
e
f t t f
t
.
1. Montrer, pour tout réel
0t
les inégalités
1
t
et
et
1 (1 ) 0
t
te
. Calculer la
dérivée de f sur ]0 ; +[, étudier les variations de f.
2. Etudier la continuité de f en 0.

3. En considérant les fonctions u et v définies sur [0 ; +[ par
2
( ) 1 2
tt
u t e t
et
23
( ) 1 26
ttt
v t e t
, montrer que, pour tout réel positif t, que
2 3 2
1
2 6 2
t
t t t
et
.
En déduire la dérivabilité de f en 0.
4. On appelle G la fonction définie sur
0;
par
2
( ) ( )
x
x
G x f t dt
. On ne cherchera pas à
calculer l’intégrale.
a) En considérant une primitive F de f, montrer que
2
'( ) xx
ee
Gx x
. En déduire les
variations de G.
b) Montrer que, pour tout t de [x ; 2x],
2
1 1 1
x t x
e e e
. En déduire que pour tout
x de
0;
,
2
(1 )ln2 ( ) (1 )ln2
xx
e G x e
et les limites de G en 0 et en +.