Géométrie dans l`espace 1 Perspective cavalière

Géométrie dans l’espace
Activité préparatoire : Construire un cube
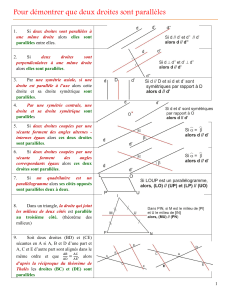
1 Perspective cavalière
Activité 1 : Dessiner un cube
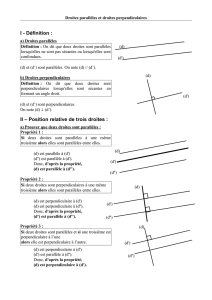
Définition 1 : On appelle plan frontal tout plan qui fait face à l’observateur.
Propriété 1 : Dans tout plan frontal, les longueurs et les angles sont respectés.
Définition 2 : On appelle fuyante toute droite perpendiculaire au plan frontal.
Propriété 2 : Les fuyantes sont dessinées avec un angle αpar rapport à l’horizontale.
Propriété 3 : Sur les fuyantes les longueurs sont multipliées par un coefficient k.
Remarque : En général on prend pour αune des valeurs 30° ou 45° ou 60° et pour k 0,5 le plus souvent.
Propriété 4 : Les faces de l’objets sont supposées opaques. Les traits vus par l’observateur sont dessinés en traits pleins ceux qui
sont cachés à sa vue sont dessinés en pointillés.
Exemple 1 : Dessiner un cube de 5 cm de côté dans une perspective cavalière d’angle α=60° et de rapport k=0,5.
A
B
C
D
E F
G
H
Remarque : Je place toujours A en bas à gauche, B en bas à droite, ABCD est la face inférieure, E est en haut à gauche.
Activité 2 : Perspective et illusion
Propriété 5 : L’image du milieu d’un segment dans la réalité est placé au milieu du segment sur le dessin. La réciproque est fausse,
un point placé au milieu d’un segment sur le dessin n’est pas forcément placé au milieu du segment dans la réalité.
Propriété 6 : Dans tout plan frontal les longueurs et les angles sont conservés. Dans les autres plans les longueurs et les angles ne
sont pas conservés.
Propriété 7 : Des droites parallèles dans la réalité sont dessinées parallèles sur le dessin en perspective. Le contraire est faux, des
droites parallèles sur le dessin ne sont pas forcément parallèles en réalité.
Propriété 8 : Des droites sécantes dans la réalité sont sécantes sur le dessin en perspective. Le contraire est faux, des droites sécantes
sur le dessin ne sont pas forcément sécantes en réalité.
Propriété 9 : Des points alignés dans la réalité sont alignés sur le dessin en perspective. Le contraire est faux, des points alignés sur
le dessin ne sont pas forcément alignés en réalité.
1

Activité 3 : Dessin d’un d’un pavé droit. Patron d’une pyramide. Observation, démonstration.
Observation d’un triangle particulier et d’une droite de ce triangle.
2 Positions relatives de droites et de plans
Propriété 10 : Deux points distincts définissent une droite.
Propriété 11 : Trois points distincts non alignés définissent un plan.
Remarque : Quatre points ne sont pas forcément dans un même plan.
Définition 3 : Si quatre points sont dans un même plan alors on dira qu’ils sont coplanaires.
Remarque : Lorsque quatre points sont coplanaires, ils sont soit alignés, soit sur deux droites parallèles, soit sur deux droites sé-
cantes. Nous dirons alors que ces deux droites sont coplanaires.
Activité 4 : Positions relatives de droites et de plan.
2.1 Position relative de deux droites distinctes(d1) et (d2)
3 situations :
(d1) et (d2) sont coplanaires (d1) et (d2) ne sont pas coplanaires
(d1) ∩(d2) = {M} (d1) ∩(d2) = ;(d1) ∩(d2) = ;
L’intersection de (d1) et (d2) est le point M.
Les droites (d1) et (d2) sont sécantes en M.
L’intersection de (d1) et (d2) est vide. (d1) et
(d2) sont strictement parallèles.
L’intersection de (d1) et (d2) est vide,
mais les droites ne sont pas parallèles.
2.2 Position relative d’une droite (d) et d’un plan (P)
3 situations :
(d) est strictement parallèle à (P) (d) est sécante à (P) en un point M (d) est incluse dans (P) : (d) ⊂(P)
(d) ∩(P) = ;(d) ∩(P) = {M} (d) ∩(P) = (d)
(d) et (P) n’ont aucun point commun. (d) et (P) ont un seul point commun. Tous les points de (d) sont des points de
(P).
Propriété 12 : Si deux points d’une droite sont dans un plan alors la droite est toute entière dans ce plan.
Propriété 13 : Une droite est parallèle à un plan si et seulement si elle est parallèle à une droite de ce plan.
2.3 Position relative de deux plans (P1) et (P2)
2 situations :
(P1) et (P2) sont parallèles (P1) et (P2) sont sécants
(P1) ∩(P2) = ;(P1) ∩(P2) = (d)
(P1) et (P2) n’ont aucun point commun (P1) et (P2) ont une droite en commun
3 Sections
3.1 Activités sur le cube
Méthode générale : Construire la section d’un solide par un plan (P) c’est construire les intersections du plan (P) avec les faces
du solide.
rem : La section obtenue est un polygone dont les côtés sont sur les faces du solide.
Méthode 1 : On cherche sur les faces du solide, deux points communs à cette face et au plan de section.
Méthode 2 : Un plan coupe deux plans paralléles selon des droites paralléles.
Méthode 3 : Pour trouver l’intersection d’une droite (d) et d’un plan, on construit l’intersection de la droite (d) et d’une droite
particulière (d’) du plan dont on sait que (d) et (d’) sont coplanaires .
Méthode 4 : Deux droites coplanaires appartenant à deux plans sécants se coupent sur la droite d’intersection des deux plans.
2

4 Autres propriétés
• Dans tout plan de l’espace les théorèmes de la géométrie plane s’appliquent.
• Pour qu’une droite soit parallèle à un plan, il suffit qu’elle soit parallèle à une droite de ce plan.
• Pour que deux plans soient parallèles, il suffit que l’un contienne deux droites sécantes parallèles à l’autre.
• Si deux droites sont parallèles alors :
– Tout plan parallèle à l’une est parallèle à l’autre.
– Toute droite parallèle à l’une est parallèle à l’autre.
– Si deux plans sont parallèles alors :
– Toute droite parallèle à l’un est paralèle à l’autre.
– Tout plan parallèle à l’un est parallèle à l’autre.
– Tout plan qui coupe l’un coupe l’autre et les droites d’intersection sont parallèles
• Si deux plans sont parallèles alors tout plan qui coupe l’un coupe l’autre et les droites d’intersection sont parallèles
• Si une droite est parallèle à deux plans sécants alors elle est parallèle à leur intersection.
3