Question 1 Durée estimée : 2min Le coefficient directeur de la droite

Classe : Première S
Matière : Mathématiques
Thème(s) abordé (s) : Nombre Dérivée
QCM
Les 5 premières questions de ce Questionnaire à Choix Multiples permettent de contrôler les
connaissances nécessaires pour appréhender les exercices.
Question 1 Durée estimée :
2min
Le coefficient directeur de la droite passant par les point A (1 ; 2) et B(3 ; 6) est égale à :
□ A:3 □ B : -3 □ C: 2 □ D :
√
2
Question 2 Durée estimée :
2min
Soit f une fonction définie sur
¡
et Cf sa courbe représentative dans un repère
orthonormé. A et B deux points de Cf de coordonnées respectives A ( a ; f(a) ) et
B ( a+h ; f (a+h) ), avec a et h deux réels donnés. Le coefficient directeur de la droite (AB)
est égal à :
f(a+h)− f(a)
h
□ Vrai □ Faux
Question 3 Durée estimée :
2min
Soit
f
la fonction carrée définie sur
¡
par :
f(x)=x2
.
f(3+h)− f(3)
h
est égal à :
□ A : 6 □ B : h+6 □ C : h2 + 3 □ D : h+3
Question 4 Durée estimée :
2min
Soit f la fonction définie sur
¡
par : f ( x ) =
x2+2 x−3
et Cf sa courbe représentative
dans un repère orthonormé. A et B deux points de Cf de coordonnées respectives
A( 1; 0 ) et B( 1+h ; f(1+h) ).La limite du coefficient directeur de la droite (AB) , lorsque h
tend vers 0 est égal à :
□ A:5 □ B : 2 □ C:-3 □ D : 4
Accompagnement scolaire et préparation aux contrôles
Toute reproduction, même partielle, sans autorisation, est strictement interdite.

Question 5 Durée estimée :
3min
La parabole ci-dessous est la représentation graphique d'une fonction f dérivable sur
¡
.
La tangente au point B( 1 ; 1) passe par le point C( 0 ; 3). f ' (1) est égal à :
□ A:3 □ B:-3 □ C:2 □ D :-2
QCM (suite)
Les 5 questions suivantes permettent d’évaluer la compréhension du thème dans sa globalité. Elles
exigent que les exercices suivants soient correctement assimilés.
Question 6 Durée estimée :
2min
Soit f une fonction dérivable en a=2 et tel que f(2) = 3 et f '(2) = -4 . L'équation réduite de
la tangente à la courbe représentative de f au point d'abscisse 2 est :
□ A : y = 2 x + 3 □ B: y = -4 x + 3 □ C: y = -4 x + 11 □ D: y = -4 x
Question 7 Durée estimée :
3min
La fonction racine carrée définie par
f(x)=
√
x
est dérivable en 1 et son nombre dérivée
en 1 , f ' ( 1 ) est égal à
1
2
□ Vrai □ Faux
Accompagnement scolaire et préparation aux contrôles
Toute reproduction, même partielle, sans autorisation, est strictement interdite.

Question 8 Durée estimée :
3min
Soit f la fonction racine carrée définie à la question 7, l'équation réduite de la tangente à
la courbe représentative de f au point d'abscisse 1 est :
□ A : y =
1
2x+1
□ B : y =
1
2x−1
□ C: y =
1
2x
□ D: y =
1
2x+1 2
Question 9 Durée estimée :
3min
D'après l'équation réduite de la tangent à la courbe représentative de la fonction racine,
au point d'abscisse 1, trouvée à la question 8 et en utilisant cette approximation affine au
voisinage de 1, on peut dire qu'une valeur approchée de
√
1,0000002
est égale à :
□ A : 1,0001 □ B : 1,0002 □ C : 1,0000001 □ D : 1,0000002
Question 10 Durée estimée :
3min
Soit f la fonction définie sur
¡
par f ( x ) =
3 x2−5 x+8
. f '( 5) est égale à :
□ A : 25 □ B : 58 □ C : 125 □ D : -58
Exercice 1 (entraînement)
Cet exercice met en relief des principales notions de cours.
Il n’a pas de difficulté particulière mais nécessite une bonne connaissance de la leçon.
On considère la fonction f définie par f(x) =
x2−x+1
1. Déterminer les coordonnées du point A d'abscisse 2 de la courbe C représentant la fonction f.
2. Calculer f(2+h) et en déduire que
f(2+h)− f(h)
h
= h+3
3. Justifier que la fonction f est dérivable en 2 et donner la valeur de f ' (2)
4. Démontrer que la droite passant par A et de coefficient directeur 3 a pour équation :
y= 3x – 3
Accompagnement scolaire et préparation aux contrôles
Toute reproduction, même partielle, sans autorisation, est strictement interdite.

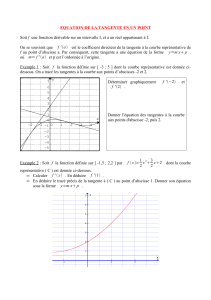
Exercice 2 (approfondissement)
Cet exercice offre la possibilité d’effectuer des raisonnements et des calculs qui imposent de bonnes
connaissances du cours et la maîtrise des techniques de résolution.
La courbe ci-dessous est la représentation graphique d'une fonction f.
1. Déterminer graphiquement f(2) et f ' (2). En déduire l'équation réduite de la tangente à la
courbe au point d'abscisse 2.
2. Déterminer graphiquement f(1) et f ' (1). En déduire l'équation réduite de la tangente à la
courbe au point d'abscisse 1.
3. Soit g la fonction inverse. Démontrer que la fonction inverse est dérivable en a = 2 et donner la
la valeur de g'(2).
Accompagnement scolaire et préparation aux contrôles
Toute reproduction, même partielle, sans autorisation, est strictement interdite.