TD Moteur à Courant Continu

TD moteur à CC
1
TD Moteur à courant continu : moteur d’axe de robot
Pour ce moteur, on définit les caractéristiques suivantes :
Equations :
Loi d’Ohm relative à l’induit : u(t) – R.i(t) – e(t) = 0
Principe fondamental de la dynamique à la partie tournante : cm(t) – cr(t) – f.ω(t) = J.dω(t)/dt
En fonctionnement linéaire : cm(t) = k.i(t) et e(t) = k.ω(t)
Etude du moteur
Q1 – On suppose cr(t)=0. Donner les images des équations par la transformation de Laplace en
considérant que le système part du repos.
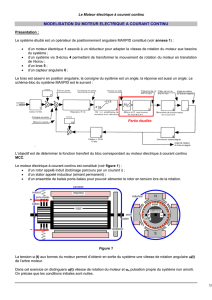
Q2 – En étudiant chaque équation, recopiez le schéma-blocs
ci-dessous sur votre feuille et complétez le.
Par exemple : E(p) = k.(p) se traduit par le bloc suivant :
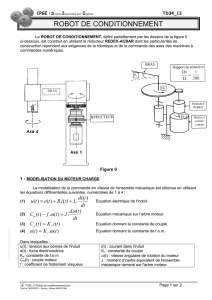
L’actionneur de l’axe 2 du robot ci-
contre est un moteur à courant
continu qui fonctionne en régime
linéaire.
Son entrée u(t) est la tension de
commande, sa sortie ω(t) est la
fréquence angulaire de rotation du
bras par rapport au corps du robot.
Il entraîne une « charge » qui le
freine, représentée par un couple
de perturbation cr(t).
R : résistance totale du circuit de l’induit,
J : inertie totale (arbre + charge),
f : coefficient de frottement visqueux produisant un
couple proportionnel à la vitesse,
i(t) : courant variable dans l’induit,
e(t) : force électromotrice induite,
cm(t) et cr(t) : couples moteur et résistant sur l’arbre.
La partie commande du système élabore la tension
d’entrée u(t) du moteur qui est transformée en une
sortie en fréquence angulaire de rotation ω(t).

TD moteur à CC
2
Q3 – Ce schéma-blocs est-il le schéma-blocs d’un système asservi ? Justifiez votre réponse.
Q4 – En écrivant les équations aux blocs (sortie = fonction*entrée), en déduire le rapport
)p(U )p(
)p(Hm
,
appelé fonction de transfert du moteur.
A partir de maintenant et jusqu’à la fin du problème, utiliser les valeurs numériques suivantes :
Km = 2 rad/(V.s) ; Tm = 0,2 s.
Les conditions initiales étant nulles, on applique à l’entrée du moteur un échelon de tension u(t)=u0.u(t)
d’amplitude u0 = 20V.
Q5 – Donner l’équation de la réponse temporelle ω(t) du système. Tracer l’allure de sa courbe
représentative en indiquant sur celle-ci toutes les grandeurs caractéristiques.
Q6 – Quelle sera la vitesse ω1 atteinte par le moteur en régime permanent. La convertir en tour/min.