TD34_13 Robot de conditionnement

CPGE / S ciences I ndustrielles pour l’ I ngénieur TD34_13
: TD34_13 Robot de conditionnement.doc- Page 1 sur 2
Créé le 14/05/2010 – Source : Mines AADN 1996
M Salette
-
Lycée Brizeux
-
Quimper
ROBOT DE CONDITIONNEMENT
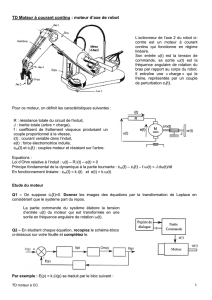
Le ROBOT DE CONDITIONNEMENT, défini partiellement par les dessins de la figure 0
ci-dessous, est construit en utilisant le réducteur REDEX-ACBAR dont les particularités de
construction répondent aux exigences de la robotique et de la commande des axes des machines à
commandes numériques.
Figure 0
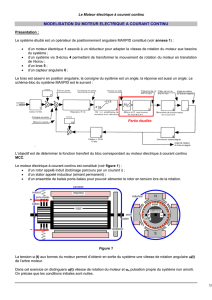
1 - MODELISATION DU MOTEUR CHARGE
La modélisation de la commande en vitesse de l'ensemble mécanique est obtenue en utilisant
les équations différentielles suivantes, numérotées de 1 à 4 :
(1)
dt
tdi
LtiRtetu )( .)(.)()( ++=
Equation électrique de l'induit.
(2)
dt
td
JtftC
m
)(
.)(.)(
ω
ω =−
Equation mécanique sur l'arbre moteur.
(3)
)(.)( tiKtC
tm
=
Equation donnant la constante de couple.
(4)
)(.)( tKte
e
ω
=
Equation donnant la constante de f.e.m.
Dans lesquelles :
u(t) : tension aux bornes de l'induit
e(t) : force électromotrice
K
e
: constante de f.e.m
C
m
(t) : couple moteur
f : coefficient de frottement visqueux
i(t) : courant dans l'induit
K
t
: constante de couple
ω(t) : vitesse angulaire de rotation du moteur
J : moment d'inertie équivalent de l'ensemble
mécanique ramené sur l'arbre moteur.

CPGE / S ciences I ndustrielles pour l’ I ngénieur TD34_13
: TD34_13 Robot de conditionnement.doc- Page 2 sur 2
Créé le 14/05/2010 – Source : Mines AADN 1996
1 - 1 - Exprimer ces quatre équations différentielles dans le domaine de Laplace. Conditions
initiales nulles.
1 - 2 - Sachant que f et L sont négligeables, compléter le schéma fonctionnel identique à celui
ci-dessous, en notant la transmittance élémentaire de chaque bloc.
1 - 3 - Déterminer la fonction de transfert en boucle fermée :
)( )(
)( pU p pH
Ω
= .
Mettre H(p) sous forme canonique, préciser l'ordre de H(p) et calculer les paramètres
correspondants sachant que :
R= 1 ohm ; J = 1,2 10
-4
kg.m
2
; K
e
= 0, 1 V/rd/s ; K
t
= 0, 1 N.m / A
2 - ASSERVISSEMENT DE POSITION
2 - 1 - Le système est matérialisé par le schéma bloc ci-dessous :
Ω(p) : Image de Laplace de la vitesse de rotation du moteur.
Ω
s
(p) : Image de Laplace de la vitesse de rotation du bras du robot.
θ
s
(p) : Image de Laplace de la position angulaire du bras du robot.
Compléter le schéma fonctionnel présenté ci-dessus en notant la transmittance élémentaire de
chaque bloc sous forme numérique.
2 - 2 - Asservissement de position angulaire du robot :
2 - 2 - 1 - Soit le schéma fonctionnel à retour unitaire ci-dessous :
K
r
Gain pur réglable
θ
s
(p) Position angulaire réelle du bras du
robot
θ
c
(p) Position angulaire de consigne du bras
- Déterminer la fonction de transfert en boucle fermée :
)( )(
)( pc ps pG
θ
θ
=
- Mettre sous forme canonique et préciser l'ordre de G(p).
- Déterminer en fonction de K
r
les paramètres correspondants Gain, Pulsation propre non
amortie ω
0
, Coefficient d'amortissement m.
2 - 2 - 2 - Déplacement du bras :
On veut déplacer le bras d'une valeur angulaire de consigne θ
c
= 30° par une excitation en échelon de
position ; le temps de réponse à 5% doit être minimal.
- Calculer K
r
.
- Calculer la position réelle du bras θ
s
en régime permanent, préciser le théorème utilisé.
- Quelle est l'erreur statique ?