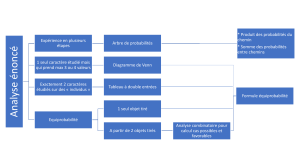
PROBABILITES CONDITIONNELLES I. Rappels sur les probabilités

PROBABILITES CONDITIONNELLES
I. Rappels sur les probabilités
1. probabilité d'un événements
Une expérience aléatoire a plusieurs issues dont la réalisation dépend du hasard.
Un événement est une issue ou un ensemble d'issues.
Propriétés :
* Une probabilité est un nombre compris entre 0 (événement impossible) et 1 (événement certain)
* la somme des probabilités des différentes issues de l'expérience aléatoire égale 1
vocabulaire:
* A un événement : on note
A
l'événement contraire de A = non A et on a :
p A=1– pA
*
2. probabilités dans une situation d'équiprobabilité
lorsque tous les cas sont équiprobables , alors pour un événement A on a:
pA= nombre de cas favorables à A
nombre decas possibles =nombre d ' éléments de A nombre total d ' éléments
=
Dans cette situation, le calcul de probabilités se ramène à un problème de dénombrement : il faut
compter “le nombre de cas favorables” et “le nombre de cas possibles”
II. . PROBABILIT2 CONJOINTE ; PROBABILIT2 CONDITIONNELLE
1. diagramme de Venn
On a la formule : p(A ∪ B) = p(A) + p(B) – p(A ∩ B)
2. ne pas confondre
A et B sont deux événements
* probabilité conjointe:
pA∩B= nombrede cas favorables à A et à B
nombrede cas possibles =nombre d ' éléments de A∩B nombre total d ' éléments
c'est la probabilité qu'un élément soit dans A et dans B
* probabilité conditionnelle:
pAB= nombre de cas favorables à B , dans A
nombre de cas possibles , dans A =nombre d ' éléments de A∩B nombre total d ' éléments de A
c'est la probabilité de B, sachant A
c'est la probabilité qu'un élément appartenant à A soit dans B
attention : ne pas confondre p(A ∩ B) et pA(B)
p(A ∩ B) est la proportion d’éléments de A ∩ B par rapport à l’ensemble total
pAB= pA∩B
pA
est la proportion d’éléments de A ∩ B par rapport au sous-ensemble A
II. . SITUATION DE DOUBLE PARTITION
1. différentes présentations
tableau à double entrée: diagramme de Venn:
A
A
total

Bp(A∩B) p(
A
∩B) p(B)
B
p(A∩
B
) p(
A
∩
B
)p(
B
)
total p(A) p(
A
) 1
arbres:
B
pA ∩ B= pA× pAB
A
B
pA ∩  B=pA× pA B
B
p A ∩ B= p A× p
AB
A
B
p A ∩  B=p A× p
A
B
A
pA ∩ B= pB× pBA
B
A
p A ∩ B= pB× pB A
A
pA ∩  B=p B× p
BA
B
A
p A ∩  B=p B× p
B
A
2. formules correspondantes
Important : les probabilités conjointes situées au bout des branches des deux arbres sont égales :
p(B∩A) = p(A∩B)
On constate les formules suivantes:
* formule des probabilités totales:
pA= pA∩B pA∩ B
)
* formules liant les probabilités conditionnelles et les probabilités conjointes :
pAB= pA∩B
pA
pA ∩ B= pA× pAB= pB× pBA
* formule des événements contraires:
pA p A=1
pABpA B=1
⇔
pA B=1−pAB