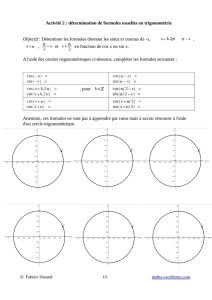
Formules de trigonométrie

Formules de trigonom´etrie
I. Introduction
Le but de cet expos´e est double
•Tout d’abord ´evidemment acqu´erir les formules de trigonom´etrie, outil indispen-
sable dans les premi`eres ann´ees du sup´erieur ; mais surtout montrer comment
on peut les assimiler et les connaˆıtre de fa¸con sˆure, sans les apprendre par coeur
mais en ayant les moyens de pallier toute d´efaillance de la m´emoire grˆace au
d´eveloppement d’un certain nombre d’automatismes.
•Ensuite montrer `a l’aide de cet exemple comment un ´el`eve peut en fin de se-
condaire faire ´evoluer ses m´ethodes d’apprentissage de fa¸con `a aborder dans de
meilleures conditions le choc de l’enseignement sup´erieur.
Premi`eres remarques
•Ces formules ne doivent pas ˆetre apprises par cœur.
•Il ne faut pas croire non plus qu’il suffit de pouvoir consulter une liste de ces
formules dans un quelconque formulaire ou dans la m´emoire de sa calculette.
Qui oserait affirmer s´erieusement qu’il est inutile d’apprendre le code de la
route et qu’il suffit d’en avoir un exemplaire `a port´ee de main pour le consulter
lorsque le besoin s’en fait sentir ?
•Il faut en apprendre le minimum et poss´eder le moyen de toutes les retrouver
imm´ediatement par des consid´erations ´el´ementaires. Il y a dans ce chapitre
quelques recettes pour vous aider `a retenir ces formules, mais les meilleures
seront celles que vous trouverez par vous–mˆeme et qui vous paraˆıtront donc les
plus naturelles.
∗Petite ´evidence : il ne s’agit pas d’apprendre par coeur ces recettes, ce qui
ne ferait que d´eplacer le probl`eme ! Vous devez assimiler la d´emarche `a
force d’utilisation, ce qui sera le cas si vous faites l’effort (ce qui ne paraˆıt
pas ´evident au d´ebut) de re-r´efl´echir les formules `a chaque utilisation, en
particulier d´ej`a lors de l’´etude de ce chapitre.
∗Ces recettes sont parfois redondantes, ce qui est une bonne chose car il est
parfois (assez souvent ?) utile d’avoir plusieurs points de vue ; d’une fa¸con
g´en´erale c’est une bonne politique que de multiplier les “instruments de
contrˆole”.
•Le meilleur moyen d’obtenir une formule exacte est de connaˆıtre sa forme
g´en´erale et, parmi les formules similaires, de savoir ´eliminer rapidement celles
qui ne conviennent pas.
Lyc´ee Priv´e Sainte Genevi`eve
1
7 septembre 2009

Formules de trigonom´ etrie — Introduction
•Le fait de re-r´efl´echir la formule `a chaque fois que l’on en a besoin peut paraˆıtre
constituer une “intol´erable perte de temps et d’´energie” mais cela permet, `a
force d’utilisations r´ep´et´ees, de bien ancrer les quelques relations indispensables
(celles qui seront encadr´ees dans la suite de ce chapitre) et ainsi d’assurer
l’ensemble des formules.
•Cette m´ethode peut `a premi`ere vue paraˆıtre moins sˆure qu’un apprentissage par
coeur, et il est ´evident que sa mise en oeuvre provoquera, au d´ebut, des erreurs
que vous n’auriez pas commises si vous ´etiez all´es voir dans un formulaire. Dites-
vous bien qu’il en a ´et´e de mˆeme lorsque vous avez commenc´e `a marcher : avant,
vous rampiez ou vous marchiez `a quatre pattes, le premier jour o`u vous avez
essay´e de marcher seulement sur vos deux jambes, vous ˆetes tomb´e, et ce ne fut
certainement pas la seule fois. Toutefois vous avez pers´ev´er´e et, aujourd’hui, la
position verticale vous semble aller de soi : c’est `a la mˆeme d´emarche que je
vous convie en ce qui concerne l’apprentissage des math´ematiques.
Cet expos´e part volontairement du niveau ´el´ementaire pour montrer comment les
contenus successifs se compl`etent en g´en´eralisant les notions vues dans les classes
ant´erieures.
Il est possible d’imprimer ce fichier pour le travailler voir >>> INDIC
Toutefois ce fichier est truff´e d’une multitude de liens hypertextes vous apportant un
peu d’aide, et cela sur plusieurs niveaux : indications, solutions et autres explications.
Pour pourvoir utiliser cette aide il faut ´evidemment avoir acc`es `a l’Internet.
Remarques :
•Pour ´eviter que le fichier principal (fichier pdf) ne se r´e-ouvre `a la premi`ere page
au retour de chacune de ces aides (petit probl`eme dˆu, je pense, `a Acrobat-
Reader), il est pr´ef´erable de le t´el´echarger et de le lancer en local sur votre
ordinateur.
•Comme ce travail est en ´evolution et que les divers fichiers, ainsi donc que
les liens entre eux, ´evoluent rapidement il est alors bon de recharger ce fichier
principal `a chaque utilisation.
Ce que vous trouverez ici est un premier jet, et toute remarque ou suggestion sera
la bienvenue. Vous pouvez m’en faire part `a [email protected]
Lyc´ee Priv´e Sainte Genevi`eve
2
7 septembre 2009

Formules de trigonom´ etrie — D´efinitions – Formules fondamentales
II. D´efinitions – Formules fondamentales
Les fonctions sin, cos et tan ont une repr´esentation naturelle `a l’aide du cercle
trigonom´etrique ou d’un triangle rectangle. On “voit” ainsi imm´ediatement de tˆete
(mais il n’est pas honteux au d´ebut de faire un dessin) certaines propri´et´es de ces
fonctions. Il serait dommage de s’en priver !
1. Le cercle trigonom´etrique (indispensable)
Dans ce qui suit, le plan ´etant rapport´e `a un rep`ere orthonorm´e direct Oxy ,
•le cercle trigonom´etrique est le cercle Γ de centre Oet de rayon 1 que l’on
oriente dans le sens inverse des aiguilles d’une montre ;
•Aest le point du plan de coordonn´ees (1,0).
Ainsi
•
•pour tout θ∈IR il existe un unique Mθ∈Γ
tel que θsoit une mesure en radian de l’angle
orient´e −→ Ox, −−→ OMθ, ce que nous ´ecrirons
plus rapidement −→ Ox, −−→ OMθ=θ;
•on d´efinit ainsi une application
φ:IR →Γ
θ7→ φ(θ) = Mθ
;
Ox
y
A
B
C
D
Mθ
θ
•´etant donn´e que la longueur de l’arc AMθest proportionnelle `a la mesure
de l’angle g´eom´etrique AOMθet que le p´erim`etre de Γ vaut 2 π, on a :
φ(2 π) = φ(−2π) = Aet donc :
∀k∈ZZ, φ(2 k π) = A
ainsi que
∀θ∈IR,∀k∈ZZ, φ(θ+ 2 k π) = φ(θ)
ce qui entraˆıne que : la fonction φest p´eriodique et 2πen est une p´eriode ;
•pour θ∈]−2π, 2π[l’arc AM a pour longueur |θ|;
•l’application φest ´evidemment surjective, ce qui signifie que pour tout M∈Γ,
il existe θ∈IR tel que M=φ(θ).
Dans la suite de ce chapitre toutes les mesures d’angles seront donn´ees en radians
et le tableau de mesures conversion suivant doit ´evidemment tenir du r´eflexe :
Angle g´eom´etrique AOB AOC AOD
Mesure en radians π
2π3π 2
Lyc´ee Priv´e Sainte Genevi`eve
3
7 septembre 2009

Formules de trigonom´ etrie — D´efinitions – Formules fondamentales
Premi`eres valeurs remarquables : Avec les notations de la figure pr´ec´edente,
•les r´eels θ=π
2et θ=−3π 2sont solutions de l’´equation φ(θ) = B;
•l’ensemble des solutions de l’´equation φ(θ) = Best π
2+ 2 k π |k∈ZZ.
Ex 1 : Donner les solutions de l’´equation φ(θ) = C.SOLUT
Ex 2 : Donner les solutions de l’´equation φ(θ) = D.SOLUT
Ex 3 : Placer sur Γ les points φ(π
4), φ(5π 4), φ(9π 4). SOLUT
2. Modulo
Dans cette partie on d´esigne par θ0,θ1et θ2trois nombres r´eels.
On a vu que φ(θ1) = φ(θ2) si, et seulement si : ∃k∈ZZ, θ2−θ1= 2 k π.
D´efinition 1
On dit que θ1est congru `a θ2modulo θ0si, et seulement si,
il existe k∈ZZ tel que : θ2−θ1=k θ0.
Notation : la relation “θ1est congru `a θ2modulo θ0” se note θ1≡θ2[θ0].
M´ethode : Il arrive souvent en trigonom´etrie d’avoir `a r´esoudre des “´equations
modulo” et la grande question est alors de savoir “s’il faut ou non diviser le modulo”.
C’est ´evidemment une fausse question et pour ´eviter toute angoise il suffit, comme
souvent, de se ramener `a la d´efinition en transformant
•une relation du type : θ1≡θ2[θ0]
•en une relation du type : il existe k∈ZZ tel que : θ2−θ1=k θ0.
comme on peut le voir (si n´ecessaire) dans la correction des exercices suivants.
Apr`es quelques utilisations de ce m´ecanisme de v´erification, on sait “si il faut ou
non” ou “pourquoi il faut” diviser, et on peut sans probl`eme sauter cette ´etape.
Ex 4 : D´eterminer les r´eels θv´erifiant : 3 θ+π≡2θ−π
3hπ 2i·
et dire combien cela donne d’images sur le cercle trigonom´etrique. SOLUT
Ex 5 : Mˆemes questions pour l’´equation : 3 θ+π≡ −2θ−π
3 hπ 2i·SOLUT
Lyc´ee Priv´e Sainte Genevi`eve
4
7 septembre 2009

Formules de trigonom´ etrie — D´efinitions – Formules fondamentales
3. Sinus, cosinus et tangente
a) D´efinition `a l’aide d’un triangle rectangle
La premi`ere d´efinition que l’on ren-
contre des lignes trigonom´etrique utilise
les angles d’un triangle rectangle.
Plus pr´ecis´ement avec les notations de la
figure ci-contre, o`u
U V
W
θ
•UV W est un triangle rectangle en V,
•θest la mesure de l’angle g´eom´etrique V U W , donc θ∈]0,π
2[,
on pose alors
cos θ=UV
UW =cˆot´e adjacent hypot´enuse et sin θ=V W UW =cˆot´e oppos´e hypot´enuse
ainsi que
tan θ=sin θ
cos θ=V W UV =cˆot´e oppos´e cˆot´e adjacent·
Comme la somme des mesures angles g´eom´etriques V UW et UW V vaut π
2, il est
imm´ediat que pour tout θ∈]0,π
2[,ona:
cos π
2−θ= sin θet sin π 2−θ= cos θ
et donc :
tan π
2−θ=1 tan θ·
Remarque : On vient ainsi de d´efinir des fonctions r´eelles d’une variable r´eelle qui,
`a tout r´eel de l’intervalle ]0,π
2[, associent un nombre r´eel.
Ex 6 : Donner les valeurs des fonctions cos, sin et tan en π
6et π 3·INDIC
Ex 7 : Donner de mˆeme en π
4les valeurs des fonctions cos, sin et tan. INDIC
Lyc´ee Priv´e Sainte Genevi`eve
5
7 septembre 2009