La trigonométrie

ABC A cos(d ABC)
d
ABC
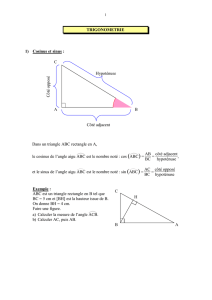
cos(d ABC) = cˆot´e adjacent
hypot´enuse =AB BC .
cˆot´e adjacent
hypot´
enuse
A B
C
−1≤cos(d ABC)≤1
¤
£
¡
¢
COS
(30 ) 0,866 10−3
¨
§
¥
¦
COS−1
¤
£
¡
¢
ACS
cos(d ABC) = 3
5d
ABC 53
ABC A
sin(d ABC)d ABC
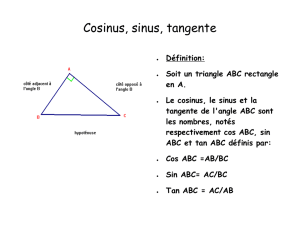
sin(d ABC) = cˆot´e oppos´e
hypot´enuse =AC BC .
cˆot´e oppos´e
hypot´
enuse
A B
C
−1≤sin(d ABC)≤1
tan(d ABC)d ABC
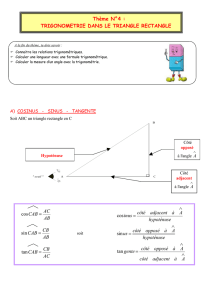
tan(d ABC) = cˆot´e oppos´e
cˆot´e adjacent =AC AB .
cˆot´e oppos´e
cˆot´e adjacent
A B
C
¤
£
¡
¢
SIN ¤
£
¡
¢
T AN
sin(30) = 0,5tan(30) = 0,577 10−3
¨
§
¥
¦
SIN −1¤
£
¡
¢
ASN
sin(d ABC) = 2
5d
ABC = 24

¨
§
¥
¦
T AN −1¤
£
¡
¢
AT N
tan(d ABC) = 1
2d
ABC = 27
(cosx)2+(sinx)2= 1
µAB
BC ¶2
+µAC
BC ¶2
= 1
d
ABC d ABC
d
ABC x
(cosx)2+ (sinx)2= 1 cos2x+sin2x= 1
tanx =sinx
cosx
cos(d ABC), sin(d ABC)et tan(d ABC)ABC
sin(d ABC)
cos(d ABC)
d
ABC x
tanx =sinx
cosx
cos sin tan
cos−1sin−1tan−1