III La Dérivation.

III La dérivation en un point –Fonctions dérivés
Page 1 sur 48 JP Huerga 16/01/2003
III La Dérivation.
La dérivation est une notion essentielle de l'analyse. Elle trouve ses origines dans un
problème purement géométrique : celui des tangentes à une courbe.
Au fil des ans, des siècles et des démonstrations, elle est devenue un outil fondamental
de l'analyse : elle permet en effet d'étudier une quantité énorme de fonctions. Et en
particulier, toutes celles qui sont vues au lycée et un peu après...
0 INTRODUCTION
Nous avons vu dans ce qui précède page 6 -7 que pour étudier le sens de
variation d’une fonction, il nous fallait trouver le ou les intervalles sur lesquels
l’ordre entre les antécédents et les images était conservé (croissance de la fonction
sur l’intervalle) ou inversé (fonction décroissante sur l’intervalle).
Une fonction f est strictement croissante sur un intervalle I de
l’ensemble de définition, si pour toutes valeurs a et b de I, si a <b alors
f(a)<f(b).
Une fonction est strictement décroissante sur un intervalle I de
l’ensemble de définition, si pour toutes valeurs a et b de I, si a <b alors
f(a)>f(b).
Une fonction est monotone sur I de l’ensemble de définition si elle ne
change pas de sens de variation sur cet intervalle.
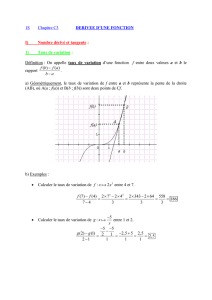
Ce qui revenait à étudier les intervalles sur lesquels le signe du taux d’accroissement
est constant.
Le taux d’accroissement étant la quantité : () ()
f
xfa
x
a
−
−
pour x et a éléments de
l’ensemble de définition. Cette quantité est en fait la pente (coefficient directeur) de la
droite passant par le point M (a ;f(a)) et N (x ;f(x)),.Cette droite s’appelle la corde MN
a
f(a)
f(x)
x
M
N
Nous pouvons remarquer que si N se rapproche de M la position limite de la corde
MN est la seconde droite tracée sur cette figure c’est la tangente à la courbe au point
M.
La difficulté principale de ce type de recherche est qu’il y a deux variables x et a et
qu’il faut déterminer les intervalles sur lesquels le rapport est constant….
Les calculs sont très vite très compliqués….C’est pour cela que fut développé la
notion de dérivé qui en prenant en compte l’aspect local des variations va nous
permettre de travailler sur une seule variable.
Pente
() ()
f
xfa
x
a
−
−

III La dérivation en un point –Fonctions dérivés
Page 2 sur 48 JP Huerga 16/01/2003
A Dérivée en un point
1
1
1
d
d
dé
é
éf
f
fi
i
in
n
ni
i
it
t
ti
i
io
o
on
n
ns
s
s
Dans cette partie, la fonction f est définie sur un intervalle I ouvert contenant le
nombre réel a .
Interprétation géométrique :
On considère les points de la courbe
représentative
M et N(; ()) (; ())afa xfx .
La quantité fx fa
x
a
() ()−
− représente le
coefficient directeur de la sécante (MN).
Explication :
Si l’on fait rapprocher N de M en suivant la courbe de f, La limite indiquée dans la Définition
1 signifie que lorsque N se rapproche de M,la corde (MN) tend à devenir la tangente à la
courbe au point M et le coefficient directeur de la droite (MN) tend vers celui de la tangente à
la courbe en A Plus le point N se rapproche du point M plus la pente de la corde se rapproche
en valeur de la pente de la tangente, la valeur de la pente de la tangente (le nombre dérivé)
est la valeur limite de ce rapprochement, c’est pour cela que nous noterons.
Remarquons que si nous remplaçons x – a par h (h est alors la valeur algébrique de
l’éloignement de en abscisse de N et M ) , alors x = a +h, f(x) = f(a+h) notre définition
devient alors :
Remarques :
A est un nombre fini et s'appelle le nombre dérivé de f en a, noté fa'( ).
Def 1 : f est dérivable en a∈R si et seulement si la courbe C de f admet au point
d’abscisse a une tangente non verticale, la pente (coefficient directeur) de cette tangente est
noté f ’(a) et s’appelle le nombre dérivé de f en a.(f ‘(a) se prononce f prime de a)
a
f(a)
f(x)
x
M
N
Def 2 : f est dérivable en a∈R si et seulement si lim () ()
xa
fx fa
xa
→
−
−=∈A où A R
Et la valeur de sa dérivé en a est f ’(a) =A
Def 3 : f est dérivable en a∈R si et seulement si lim ()()
h
fa h fa
h
→
+
−
=∈
0A où A R.
Tangente à la
courbe au
point M
Pente f ’(a)

III La dérivation en un point –Fonctions dérivés
Page 3 sur 48 JP Huerga 16/01/2003
Ce nombre est le coefficient directeur (on dit aussi la pente) de la tangente à la courbe
représentative de f au point d'abscisse a.
L’équation de la tangente à la courbe au point d’abscisse a est donc l’équation de
la droite passant par la point M (a ;f(a)) et de coefficient directeur f ‘(a)
Cette équation est donc :
Y = f ‘ (a) (x – a) + f(a)
2
2
2
N
N
No
o
om
m
mb
b
br
r
re
e
e
d
d
dé
é
ér
r
ri
i
iv
v
vé
é
é
e
e
en
n
n
a
a
a
e
e
et
t
t
t
t
ta
a
an
n
ng
g
ge
e
en
n
nt
t
te
e
e
à
à
à
l
l
la
a
a
c
c
co
o
ou
u
ur
r
rb
b
be
e
e
a
a
au
u
u
p
p
po
o
oi
i
in
n
nt
t
t
d
d
d’
’
’a
a
ab
b
bs
s
sc
c
ci
i
is
s
ss
s
se
e
e
a
a
a
Propriété :
Soit f une fonction dérivable sur un intervalle non réduit à un point contenant a
La courbe de f admet une tangente au point M(a ;f(a)) d’équation
Y = f ‘ (a) (x – a) + f(a)
Attention à la réciproque si une courbe représentative d’une fonction admet une
tangente en un point d’abscisse a elle sera dérivable en ce point à la condition que la tangente
ne soit pas verticale (c'est-à-dire quelle admette une pente finie).
Le nombre dérivé en a donne une idée quantitative de la variation de la fonction autour
de la valeur a de x, c'est-à-dire il dit de combien « penche » la courbe au point d’abscisse a.
Constatations et remarques :
Nous savons intuitivement qu’au voisinage d’un point une courbe (régulière sans sauts ou
accidents) est très proche de sa tangente en ce point. (la courbe semble « accompagner » sa
tangente près du point de tangence.
Première conséquence :
y
Tangente en A
A
Courbe C
Il parait naturel que si la tangente à une courbe (régulière) est « montante » (c'est-à-dire a une
pente positive) la courbe doit être « montante » elle aussi autour du point de tangence (c'est-à-
La courbe et sa
tangente sont très
proches l’une de
l’autre autours de A

III La dérivation en un point –Fonctions dérivés
Page 4 sur 48 JP Huerga 16/01/2003
dire qu’elle doit être issue d’une fonction croissante en ce point). Il suffit pour s’en
convaincre de regarder le dessin si dessus.
De même
Il parait naturel que si la tangente à une courbe (régulière) est « descendante » (c'est-à-dire a
une pente négative) la courbe doit être « descendante » elle aussi autour du point de tangence
(c'est-à-dire qu’elle doit être issue d’une fonction décroissante en ce point). Voir le dessin ci-
après :
y
Tangente en A
A
Courbe C
Deuxième conséquence :
La tangente en un point A ‘(a ; f(a)) à une courbe (régulière) représentative d’une fonction
numérique f est très proche de la courbe au voisinage de A peut se traduire par la fonction
affine de laquelle est issue la tangente est une bonne approximation locale des valeurs de la
fonction pour x voisin de la valeur a.
C'est-à-dire f(x) ≈ f ‘(a) (x – a) + f(a) pour x proche de a
Ou f(x+h) ≈ h f ‘ (a) +f(a) pour h proche de 0
Ces deux conséquences sont la base de l’utilisation des dérivées il faudra les garder
présentes à l’esprit.
La courbe et sa tangente
en A sont descendantes
toutes deux au voisinage
du point A et elles sont
proches l’une de l’autre

III La dérivation en un point –Fonctions dérivés
Page 5 sur 48 JP Huerga 16/01/2003
Exemples plus pratique sur la dérivation en un point (cette méthode n’est exigible que pour
les sections scientifiques)
Exemple 1
Déterminons le nombre dérivé en x = 1 de la fonction f définie par :
f(x) = 2.x2 + 1
Pour trouver ce nombre, nous allons suivre la définition d'un nombre dérivé : nous allons
étudier la limite lorsque x tend vers 1 du quotient .
Sous cette forme, le quotient n'est pas très exploitable. Nous devons donc en modifier
l'écriture.
Pour tout x différent de 1, on peut écrire que :
Donc lorsque x tend vers 1, le quotient tend vers 2 × (1 + 1) = 4.
Conclusion : la fonction f(x) = 2.x2 + 1 est dérivable en x = 1. Le nombre dérivé de
cette fonction en 1 vaut 4.
Autrement écrit :
f'(1) = 4.
Exemple 2
Déterminons le nombre dérivé en x = 0 de la fonction racine g définie par :
g(x) =
Pour parvenir à ce but, il nous faut étudier la limite lorsque x tend vers 0 du quotient
.
Pour tout réel non nul x, on peut écrire :