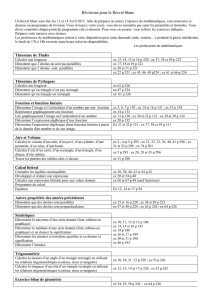
2 et en 0 et a pour tableau de variations : −6 −1 2 6 1

Séance n°3
Exercice 1.
a. Existe-t-il un réel  tel que  > 0 et √ >  ?
b. Le couple (2 − 1 ;2) est-il solution du système  = 2 + 2
 =  +1+2 ?
c. Le couple √2−1;√2 + 1  est-il solution du système  =  + 2
 = 3−√2
Exercice 2.
Dans le plan muni d’un repère, on considère les droites Δ, Δ et Δ
d’équations respectives :  = 2− ,  = 
 et  = − +1.
a. Montrer que ces droites sont parallèles.
b. Soit  un réel non nul et soit  le point de coordonnées 
; .
Montrer que le point  appartient à la droite Δ.
c. On considère les droites Δ et Δ′ d’équations respectives :
 = √2+1 + 1 et  = 
√ −1.
Montrer que ces droites sont parallèles.
d. Étudier l’intersection des droites Δ et Δ.
e. Existe-t-il un réel  pour lequel le point  appartient à la droite Δ ? et à la
droite Δ′ ?
Exercice 3.
Le plan est muni d’un repère (,,).
a. Déterminer l’ensemble ℰ des points  de coordonnées (;) telles que
+= 0.
b. Déterminer l’ensemble  des points  de coordonnées (;) telles que
( +)= +.
Exercice 4.
Écrire les contraposées des propositions suivantes et les démontrer sachant que 
est un entier naturel,  et  sont des nombres réels.
1. Si  est un nombre premier supérieur ou égal à 3 alors  est impair.
2. Si  ≠ 0 alors  ≠ 0 et  ≠ 0.
3. Si  ≠  alors ( +1)(−1)≠ ( − 1)( + 1) .
Exercice 5.
La fonction  s’annule en −2 et en 0 et a pour tableau de variations :
−
6
−
1
2
6
1
5
−
3
2
Quel est son signe ?
Exercice 6. QCM
Le plan est muni d‘un repère orthonormé (0,,). On considère les points
(−4;−2), (−1;3) et (7,−2) et les vecteurs 
(−2;5) et (3;0).
1. Le vecteur −3 + 2 a pour coordonnées :
a. (−3 ;2) b. (5 ;−5) c. (0 ;−15) d. Autre
2. Une expression de  − +2 − est :
a.  b.  c. 0 d. Autre
3. Un quadrilatère  est un parallélogramme si et seulement si :
a.  =  b.  =  c.  =  d. Autre
4. Le point  est le milieu du segment [] si et seulement si :
a.  + =  b.  =  c.  + = 0 d. Autre
5. Les coordonnées du vecteur  sont :
a. (5;3) b. (−3;5) c. (−5;1) d. Autre
6. La longueur  est égale à :
a. √34 b. √8 c. √26 d. Autre
7. Le triangle  est :
a. rectangle en A b. rectangle en B c. quelconque d. Autre
8. Les coordonnées du milieu  du segment [] sont :
a. 
,0 b. − ,  c.  ,−2 d. Autre
9. Les coordonnées du centre de gravité  du triangle  sont :
a. 
,−  b. − ,1 c.  ,−  d. Autre
10. Les coordonnées du point  tel que  soit un parallélogramme sont :
a. (10,3) b. (4,−7) c. (−12,−3) d. Autre

Séance n°3
Exercice 7.
1. Le produit de deux nombres pairs est-il pair ?
2. Le produit de deux nombres impairs est-il impair ?
3. Le produit d’un nombre pair et d’un nombre impair est-il pair ou impair ?
4. Un nombre entier est-il pair si et seulement si son carré est pair ?
Exercice 8.
a. Il existe un réel  tel que pour tout réel , on a  + > 0.
b. Pour tout réel , il existe un réel  tel que  + > 0.
c. Il existe un réel  tel que pour tout réel , on a > .
d. Il existe un réel  tel que pour tout réel , on a < .
1. Les propositions précédentes sont-elles vraies ou fausses ?
2. Donner leurs négations.
Exercice 9.
1. Donner si possible trois antécédents de −
, de −1 et de −2 par la fonction
cosinus.
2. On considère la fonction  définie sur ℝ par ()=()
 ().
a. Pourquoi la fonction  est-elle bien définie sur ℝ .
b. Donner les images de 
 ,  , −  et  par la fonction .
Exercice 10.
On souhaite démontrer que les médianes d’un triangle sont concourantes et
situer leur point de concours (le centre de gravité).
On considère un triangle  et on note ,  et  les milieux respectifs des
segments [], [] et [].
1. Donner les coordonnées des points , , , ,  et  dans le repère ( ;,).
2. On appelle  le point de coordonnées 
;  dans ce repère.
a. Démontrer que les points ,  et  sont alignés.
b. Démontrer de même que les points ,  et  sont alignés et qu’il en est
de même pour les points ,  et .