Exercice I (6 pts). Exercice II (7 pts): champ champ électrique

Page 1 sur 2
Les rappels
mathématiques,
A re
mettre
Exercice I (6 pts).
En coordonnées sphériques
+
→
+
→
=
→
∇
∂∂ ∂∂ ∂
∂
θ
ϕ
θθ sin
1
u
1
urrr
r
Démontrer que :
=
→
•
→
∇r A2
1
∂∂
=
→
∧
→
∇
ϕ
θ
θθ
)
sin(
sin
1A
r
A
Exercice II (7 pts):
champ
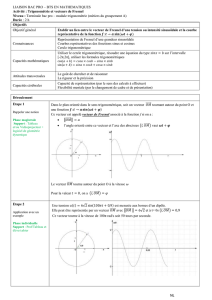
Un anneau de rayon R, situé dans le plan
densité linéique homogène, λ ,
algébrique
repéré sur l’anneau par le
vecteur position
position
→
r repère un point P
quelconque
On pose a = r/R : rayon relatif ,
r
1.
Etablir la forme intégrale de l’expression du
uniformément chargé.
2. En déduire
la grandeur du champ
= π /2 en fonction de k λ
/R
3. Tracez alors E=f(a)
avec a compris entre 0 et 2
Devoir n° 01
mathématiques,
l’électrostatique et la magnétostatique
mettre
avant jeudi, le 15/10/2015 a 10 : 00 AM
--------------Note/20---------------
En coordonnées sphériques
, l’ opérateur différentiel nabla ,
→
∇
, est
→
ϕ
ϕ
u
. Soit
→
A
un vecteur quelconque:
=
→
A
ϕ
ϕ
θ
θ
θθ
θ
∂
∂
+
∂∂
+
∂
∂A
rr
r
r
AA
r
sin
1
)(sin
sin
1
2
( )
et que
→→ +
∂
∂
−
∂
∂
+
∂
∂
−
θϕ
θ
θ
ϕθϕ
1
u)(sin
sin
1
u
)
r
r
r
rA
r
A
r
A
champ
électrique - hors axe - d’un anneau.
Un anneau de rayon R, situé dans le plan
Oxy , de centre O , d'axe Oz
est uniformément chargé par une
algébrique
c.-à-d. λ >0 ou λ < 0. Un élément
infinitésimal
vecteur position
→
'r faisant un angle α
arbitraire avec l’axe
quelconque
dans l’espace.
r
varie allant de 0 à l’ ∞ , a = 1 à r = R .
Etablir la forme intégrale de l’expression du
champ électrostatique
→
E
créé
la grandeur du champ
dans le plan Oxy de l’anneau
au point de coordonnées
/R
où k=1/(4 πε
0
) .
avec a compris entre 0 et 2
par pas de 0,1 et θ = π /2 .
λ
(D)
O
Prof. : B. SAAD
l’électrostatique et la magnétostatique
, est
le suivant :
→
+
→
+
→
=
ϕθ
ϕθ
uuu AA
r
A
r
et que
→
∂
∂
−
∂
∂
ϕθ
θ
u)(
1
r
A
rA
r
r
est uniformément chargé par une
infinitésimal
de charge dq est
arbitraire avec l’axe
Ox . Le vecteur
créé
au point P par l’anneau
au point de coordonnées
a=1/2, θ
P

Page 2 sur 2
Exercice III (7 pts). L
e Potentiel vecteur d’un
Considérons une boucle de courant circulaire, de rayon
sens trigonométrique. La boucle est située dans le plan
1.
Démontrer que le potentiel vecteur en un point P loin de la boucle peut se mettre sous la forme
2r0
rum 4
A
→→
→
∧
=
π
µ
où
→
m
est le
2.
Calculez le vecteur densité de flux magnétique,
potentiel vecteur
→
A .
3. Calculer →→ ∧∇ A et →→ ∧∇ B .
x
→
'
r
P
Prof.
e Potentiel vecteur d’un
dipôle magnétique.
Considérons une boucle de courant circulaire, de rayon
a
, parcourue par un courant
sens trigonométrique. La boucle est située dans le plan
Oxy.
Démontrer que le potentiel vecteur en un point P loin de la boucle peut se mettre sous la forme
est le
moment magnétique. Donner l’expression de
→
m
Calculez le vecteur densité de flux magnétique,
→
B
, créé par la boucle au point P utilisant le
*****
θ
r
u
→
a
ϕ
→
u
ϕ
z
r
u
→
ϕ
→
u
I
→
ld
→
r
α
Prof.
: Bendaoud SAAD
dipôle magnétique.
, parcourue par un courant
I stationnaire dans le
Démontrer que le potentiel vecteur en un point P loin de la boucle peut se mettre sous la forme
→
m
et son unité.
, créé par la boucle au point P utilisant le
ϕ
y
θ
→
u