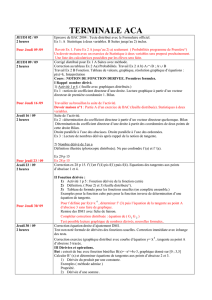
DS Mercredi 28 septembre 2016. BTS CM n°1 : On a tracé la courbe

DS Mercredi 28 septembre 2016. BTS CM
n°1 : On a tracé la courbe d'une fonction f et ses tangentes en 1 et en – 2 et la courbe
d'une fonction g et ses tangentes en –1 et en 3.
a. Lire graphiquement : f( –2) ; f(0) ; g( –1) et g(3).
b. Dire à quoi correspond le nombre dérivé de f graphiquement.
c. Lire graphiquement : f '( –2) ; f ' (0) ; g ' ( –1) et g ' (3).
n°2 : On considère la fonction f(x) = x3 – 3 x2 – 45 x – 2. ( x un nombre réel)
a. Calculer la fonction dérivée de f.
b. Etudier le signe de la dérivée de f dans un tableau de signe.
c. En déduire le tableau de variations de f et le compléter.
d. Tracer sur votre calculatrice la courbe de f
avec une fenêtre variant de
– 10 à 10 en abscisse
et de – 200 à 100 en ordonnée.
Recopier l'allure obtenue ci-contre.
e. Quel est le nombre de solutions de l'équation f(x) = 0 ?
Donner un encadrement à 0,1 près de chaque solution.
n°3 : On considère la fonction g(x) = 1 + 3x – 5x2
a. Calculer la fonction dérivée de g.
b. Etudier le signe de g '(x) dans un tableau.
c. En déduire le tableau de variation de g.
d. Calculer g(0) et g '(0) ;
en déduire une équation de la tangente en 0 à la courbe de g.
Rappel du cours : la tangente en a à la courbe de g a pour équation :
y = g '(a)( x – a) + g(a).
n°4 : Calculer la fonction dérivée de f, simplifier au maximum.
a. f(x) = 
 b. f(x) =   c. f(x) = 
Rappel du cours : la dérivée de 
 est égale à 
Barème :
n°1 : a. 1 b. 0,5 c. 2 Total : 3,5 points
n°2 : a. 1 b. 2 c. 1 d. 0,5 e. 0,5 + 1,5 Total : 6,5 points
n°3 : a. 1 b. 1,5 c. 1 d. 1,5 Total : 5 points
n°4 : a. 1,5 b. 1,5 c. 2 Total : 5 points
TOTAL sur 20 points :

DS Mercredi 28 septembre 2016. Correction BTS CM
n°1 : On a tracé la courbe d'une fonction f et ses tangentes en 1 et en – 2 et la courbe
d'une fonction g et ses tangentes en –1 et en 3.
a. f( –2) = 4 ; f(0) = 1 ; g( –1) = – 2 et g(3) = 5.
b. Le nombre dérivé de f en a correspond au coefficient directeur de la tangente en a.
c. Lire graphiquement : f '( –2) = 
 ; f ' (0) =  ; g ' ( –1) =   et g ' (3) = 
n°2 : On considère la fonction f(x) = x3 – 3 x2 – 45 x – 2. ( x un nombre réel)
a. f '(x) =    
b.et c. on résout f '(x) = 0       
polynôme du second degré :  = b² – 4ac = (-6)² – 4×3×(-45) = 36 + 540 = 576
 = 24 deux solutions x = 
ou x = 
f(-3) = 33 – 3×3² – 45×3 – 2 = 79 et f(5) = … = – 177
d.
e. L'équation f(x) = 0 admet 3 solutions.
une entre – 6 et – 5
une entre – 1 et 0 et une entre 8 et 9.
Encadrement à 0,1 près de chaque solution :
– 5,4 < x1 < – 5,3 ; – 0,1 < x1 < 0 ; 8,3 < x1 < 8,4
n°3 : On considère la fonction g(x) = 1 + 3x – 5x2
a. g '(x) = 3 – 10 x
b. et c. on résout g '(x) = 0  3 – 10 x = 0  3 = 10 x  
signe de a = -10 à
droite de zéro
g(0,3) = 1 + 3 × 0,3 – 5 × 0,3² = 1,45
d. g(0) =1 + 3×0 – 5×0² = 1 et et g '(0) = 3 – 10×0 = 3
Tangente en 0 à la courbe de g : y = g '(0)(x – 0) + g(0) : y = 3 x + 1
n°4 : a. f(x) = 
 f '(x) = 
b. f(x) = 
 f '(x) = 
c. f(x) = 
 f '(x) = 
pour le n°4 : il faut détailler le calcul, ce que je n'ai pas fait ici ‼!
x
–  – 3 5 +
signe de f '(x)
+ 0 – 0 +
variations
de f
79
– 177
x
–  0,3 +
signe de g '(x)
+ 0 –
variations
de g
1,45