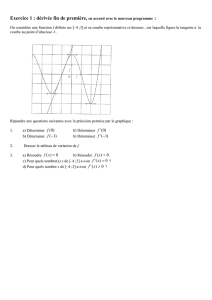
Dérivée et équation réduite de la tangente à la courbe

C PELLERIN
Dérivée et équation réduite de la tangente à la courbe
En chaque point d’une fonction dérivable, on peut calculer le nombre dérivé et
déterminer l’équation réduite de la tangente.
Cette équation a TOUJOURS la même forme y = ax + b
a est le coefficient directeur de la tangente ET le nombre dérivé de la fonction en un
point
b est l’ordonnée à l’origine
Exemple : Soit f(x) = 3  la fonction définie sur l’intervalle [-2 ; 6]
1- Calculer la dérivée f’ de la fonction f
2- Calculer f’(4)
3- Déterminer l’équation réduite de la tangente à la courbe au point d’abscisse
xC = 4
Résolution de l’exercice
1- Si f(x) = 3  alors f’(x) = 3 
Que l’on peut aussi écrire f’(x) = 
2- On pose x = 4 et on remplace dans le calcul de la dérivée
f’(4) = 
 f’(4) = =   car    f’(4) = 
3- Pour déterminer l’équation de la droite, on a besoin de procéder par étapes :
 Calcul des coordonnées de C, point d’abscisse xC = 4 (voir énoncé)
XC = 4, on connaît déjà l’abscisse, pour déterminer l’ordonnée, on doit remplacer xC
dans l’équation DE LA FONCTION.
f(4) = 3 f(4) = 3x2 f(4) = 6
Le point C a donc pour coordonnées C (4 ; 6)
 L’équation de la tangente à la courbe a pour forme y = ax + b
On connaît déjà a, car le coefficient directeur de la droite est aussi le nombre dérivé.
Donc on peut déjà écrire y = 
On trouvera maintenant b grâce aux coordonnées du point C car ce point appartient
à la droite, ces coordonnées vérifient l’équation :
yC = 
    6 = 3 + b b = 3
L’équation de la tangente à la courbe au point d’abscisse xC = 4 est :
y = 0,75x + 3