Planètes

Proposition de correction du sujet des Mines de Douai 2007
(épreuve commune)
Exercice de Mécanique - Planètes
réalisée par B. Louchart, professeur au lycée E. Woillez de Montreuil-sur-mer (62)
et colleur en Maths Sup MPSI et Maths Spé MP au lycée Mariette de Boulogne-sur-mer (62)
© http://b.louchart.free.fr
référentiel : lié à l'étoile, considéré galiléen
système : planète P
1.
f
r
= –
2Pe
r
M M G
r e
r
2. D'après le théorème du moment cinétique,
dt
Ld
O
r
= M
O
(
f
r
) = OP ∧
f
r
= 0
r
car OP //
f
r
⇒
L
r
= OP ∧ M
P
P
v
r
est constant au cours du temps
⇒ OP ∧
P
v
r
= C
r
, où C
r
est constant
⇒ OP C
r
⇒ P se déplace dans le plan orthogonal à C
r
passant par O
⇒ le mouvement est plan (plan passant par O et perpendiculaire à (Oz))
Le mouvement est circulaire
⇒ v
r
=
r
&
r
e
r
+ r
θ
&
θ
e
r
L
r
= OP ∧ M
P
P
v
r
= M
P
(
)
[
]
e re r e r
rr θ
θ+∧
r
&
r
&
r
= M
P
r
2
θ
&
z
e
r
⇒ L = M
P
r
2
θ
&
3.1. D'après la relation fondamentale de la dynamique, M
p
a
r
=
f
r
Le mouvement est circulaire ⇒ r = cte = R ⇒
a
r
= – R
2
θ
&
r
e
r
+ R
θ
&&
θ
e
r
Or v
c
= R
θ
&
⇒
a
r
= –
R
v
2
c
r
e
r
+
dt
dv
c
θ
e
r

⇒ M
p
–
R
v
2
c
= –
2Pe
R
M M G
dt
dv
c
0
dt
dv
c
= 0 ⇒ v
c
est constante
–
R
v M
2
cp
= –
2Pe
R
M M G
⇒
2
c
v
=
R
M G
e
⇒ v
c
=
R
M G
e
3.2. La planète parcourt, à vitesse constante, la distance d = 2πR pendant une durée ∆t = T
⇒ T =
c
vR 2
π
=
R
GM
R 2
e
π
= 2π
e
3
GM R
⇒ T
2
=
e
32
GM R4π
⇒
3
2
R
T =
e
2
GM 4π 3
ème
loi de Kepler
3.3. v
c
= R M G
e
⇒
6
c
v
=
3
3
e
3
R
MG = G
3
3
e
M
×
2
e
2
TGM 4π =
2
2
e
22
T
MG4π
⇒ v
c
= 3e
T GM2
π
3.4. E
c
=
2
1
M
p
2
c
v
=
2
1
M
p
3/2
e
T GM2 
π
E
p
= –
R
M M G
Pe
= – M
p
2
c
v
E
m
= E
c
+ E
p
=
2
1
M
p
2
c
v
– M
p
2
c
v
= –
2
1
M
p
2
c
v
= –
2
1
M
p
3/2
e
T GM2 
π
⇒

4.1. e
r
= –
v
MGM
L
pe
r
+
θ
e
r
⇒
dt
ed
r
= –
MGML
pe
dt
vd
r
+
dt
ed
θ
r
Or
dt
ed
θ
r
= –
θ
&
r
e
r
et d'après la relation fondamentale de la dynamique, M
p
dt
vd
r
=
f
r
= –
2Pe
r
M M G
r e
r
⇒
dt
vd
r
= –
2e
r
M G
r e
r
On obtient donc :
dt
ed
r
= –
MGML
pe
×
−
2e
r
M G
r e
r
–
θ
&
r
e
r
=
rML
2
p
r
e
r
–
θ
&
r
e
r
Or on a montré à la question 2. que L = M
P
r
2
θ
&
⇒
dt
ed
r
=
θ
&
r
e
r
–
θ
&
r
e
r
= 0
r
⇒ le vecteur e
r
est constant
4.2.
e
r
.
θ
e
r
=
+−
θ
e v
MGML
pe
r
r
.
θ
e
r
= –
v
MGM
L
pe
r
.
θ
e
r
+ 1 = 1 –
pe
MGML
× r θ
&
Or L = M
P
r
2
θ
&
⇒ r
θ
&
=
rM
L
p
On obtient ainsi : e
r
.
θ
e
r
= 1 –
rMGM
L
2
pe
2
–
݁
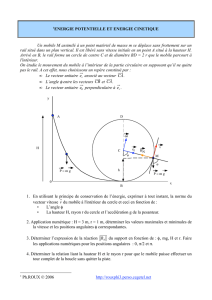
Ԧ
θ

D'après le schéma, (– e
r
).
θ
e
r
= e cos θ ⇒ e
r
.
θ
e
r
= – e cos θ
⇒ – e cos θ = 1 –
rMGM
L
2
pe
2
⇒ 1 + e cos θ =
rMGM
L
2
pe
2
⇒ r =
) cos e1(MGM L
2
pe
2
θ+×
⇒ r =
θ+
cos
e
1
p
, avec p =
2
pe
2
MGM
L
4.3. Pour une trajectoire circulaire, e = 0
4.4.
L
r
= OP ∧ M
P
P
v
r
Pour un mouvement circulaire, à tout instant, le vecteur vitesse P v
r
est perpendiculaire au vecteur
position
r
r
= OP
De plus, r = cte = R
⇒ L = M
p
R v
c
 Pour un mouvement circulaire,
e
r
=
0
r
et
v
r
= v
c
θ
e
r
⇒ –
pe
MGML
v
c
θ
e
r
+
θ
e
r
=
0
r
⇒ –
pe
MGML
v
c
+ 1 = 0 ⇒ v
c
=
L
MGM
pe
=
cp
pe
RvM
MGM
=
c
e
Rv
GM
⇒
2
c
v
=
R
GM
e
⇒ v
c
=
R
GM
e