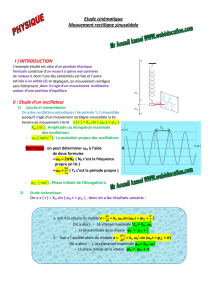
Effet Faraday et isolateur optique

−→
E(z)eiωt =−→ E0e−ikz eiωt
Bstat−→ uz
n
ω0
−→
P(z)
−→
P(z)−→ E(z)
Px(z)
Py(z)
Pz(z)
=0
χ0
1−u2−iχ0u 1−u20
iχ0u
1−u2
χ0
1−u20
0 0 χ0
Ex(z)
Ey(z)
Ez(z)
ω2
p=ne2
m0χ0=ω2
p
ω2
0−ω2ωc=eB0
mu=ωωc
ω2
0−ω2
∆−→ E(z, t)−
1 + χ0
1−u2−iχ0u 1−u20
iχ0u
1−u21 + χ0 1−u20
0 0 1 + χ0
1
c2
∂
∂t2
−→
E(z, t)=0
k ω
•
n−=q1 + χ0
1−u2−χ0u 1−u2n+=q1 + χ0 1−u2+χ0u 1−u2
−→
uxL
•
•
n+−n−
2
ωL
c=π 4
z
z
•
•
•
•
•
•
•

−ω2−→ r(z) = −ω2
0
−→
r(z)−e
m
−→
E(z)−ieω
m
−→
r(z)∧−→ B0
−→
P(z)dτ =ndτ(−e)−→ r(z)ω2
0−ω2−→
P(z) + ieω
m
−→
P(z)∧−→ B0=ne2
m
−→
E(z)
ω2
0−ω2Px(z) + iωcωPy(z) = 0ω2 pEx(z)
ω2
0−ω2Py(z)−iωcωPx(z) = 0ω2 pEy(z)
ω2
0−ω2Pz(z) = 0ω2 pEz(z)
ω2
0−ω2iωcω
−iωcωω2
0−ω2
=ω2
0−ω22−ω2ω2
c
Px(z) = 
0ω2
pEx(z)iωcω
0ω2
pEy(z)ω2
0−ω2
(ω2
0−ω2)2−ω2ω2
c
=0
ω2
pω2
0−ω2
(ω2
0−ω2)2−ωωc
Ex(z)−i0
ωcωω2
p
(ω2
0−ω2)2−ω2ω2
c
Ey(z)
Py(z) = 
ω2
0−ω20ω2
pEx(z)
−iωcω 0ω2
pEy(z)
(ω2
0−ω2)2−ω2ω2
c
=i0
ωcωω2
p
(ω2
0−ω2)2−ω2ω2
c
Ex(z) + i0
ω2
pω2
0−ω2
(ω2
0−ω2)2−ωωc
Ey(z)
ω2
p(ω2 0−ω2)
(ω2
0−ω2)2−ω2ω2
c
=χ0(ω2
0−ω2)2
(ω2
0−ω2)2−ω2ω2
c
=χ0
1−u2
ωcωω2
p
(ω2
0−ω2)2−ω2ω2
c
=χ0
ωcω(ω2
0−ω2)
(ω2
0−ω2)2−ω2ω2
c
=χ0u
1−u2
1 + χ0
1−u2ω2−c2k2−iχ0u 1−u2ω2
iχ0u
1−u2ω21 + χ0 1−u2ω2−c2k2
E0,x
E0,y =
0
1 + χ0
1−u2ω2−c2k2−iχ0u 1−u2ω2
iχ0u
1−u2ω21 + χ0 1−u2ω2−c2k2
=
01 + χ0
1−u2−k2 ω2c22
=χ0u
1−u22
−→
u±=−→ ux±j−→ uy
−→
E(0, t) = E0
2ejωt (−→
u++−→ u−)−→ E(L, t) = E0
2ejωt e−j2π
λ0n+L−→
u++e−j2π
λ0n−L−→
u−=
E0e−jn++n−
2
ωL
c
cos n+−n−
2
ωL
c
sin n−−n+
2
ωL
c
0
−→
ux
−→
u0
z=−−→
uz
−→
u0
y=−−→
uy
−−−→
Bstat =−Bstat
−→
u0
zu0=ωωc
ω2
0−ω2=−u
n+n−θ0−→ u0
x,−→
u0
yθ
−→
ux,−→ uy
z−→ ux
−θ
4−→
uy