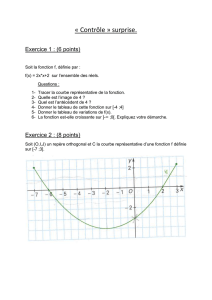
COURBES ALGEBRIQUES

COURBES
ALGEBRIQUES
Bernard Le Stum
(UniversitŽ de Rennes I)

Bernard Le Stum - Courbes AlgŽbriques - Sommaire (4/06/99)

Bernard Le Stum - Courbes AlgŽbriques - Sommaire (4/06/99)
Contenu
Introduction . . . . . . . . . . . . . . . . . . . . . . . . . 3
Chapitre O. . . . . . . . . . . . . . . . . . . . . . . . . . 5
Chapitre I . . . . . . . . . . . . . . . . . . . . . . . . . . 15
Exercices . . . . . . . . . . . . . . . . . . . . . . . . 29
CorrigŽs . . . . . . . . . . . . . . . . . . . . . . . . 34
Chapitre II . . . . . . . . . . . . . . . . . . . . . . . . . 40
Exercices . . . . . . . . . . . . . . . . . . . . . . . . 55
CorrigŽs . . . . . . . . . . . . . . . . . . . . . . . . 60
Chapitre III . . . . . . . . . . . . . . . . . . . . . . . . . 65
Exercices . . . . . . . . . . . . . . . . . . . . . . . . 82
CorrigŽs . . . . . . . . . . . . . . . . . . . . . . . . 89

Bernard Le Stum - Courbes AlgŽbriques - Introduction (4/06/99)
INTRODUCTION
Soit F ‘ È[X]Êde degrŽ d et N le nombre de solutions, Žventuellement infini,
de l'Žquation
a ‘ È, F(a) = 0.
On sait que N est fini si F ≠ 0 et qu'alors N ≤ d. En fait, on a N = dÊsi on tient
compte
1) des solutions imaginaires
2) de leurs multiplicitŽs
Soit maintenant, F et G ‘ È[X, Y]Êde degrŽs respectifs d et e et N le nombre
de solutions, Žventuellement infini du syst•me d'Žquations
(a, b) ‘ È2, 
F(a,b)=0
G(a,b)=0.
Nous allons montrer que N est fini si F et G n'ont pas de facteurs communs et
qu'alors N ≤ de. En fait, nous montrerons que N = deÊsi on tient compte
1) des solutions imaginaires
2) de leur multiplicitŽ
3) des points ˆ l'infini.
Afin de dŽmontrer ce thŽor•me, il est nŽcessaire de dŽvelopper la thŽorie des
syst•me d'Žquations polynomiales, c'est ˆ dire la gŽomŽtrie algŽbrique affine, sur
un corps (infini). De plus, puisqu'il faut donner un sens ˆ la notion de point ˆ
l'infini, il faut aussi dŽvelopper la gŽomŽtrie algŽbrique projective. Enfin, il faut
dŽfinir et Žtudier la notion de multiplicitŽ (invariant numŽrique), ce qui se fait
par l'intermŽdiaire de la notion d'anneau local en un point (invariant algŽbrique).
Dans le chapitre 0, nous rappelons quelques notions de base de gŽomŽtrie
classique, de topologie et d'alg•bre commutative. Dans le chapitre I, nous dŽve-
loppons la thŽorie sans utiliser d'alg•bre commutative. Dans le chapitre II, nous
Žtablissons le lien entre les notions dŽveloppŽes dans le chapitre prŽcŽdent et
l'alg•bre commutative. Enfin, dans le chapitre III, nous Žtudions les courbes al-
gŽbriques planes sur un corps algŽbriquement clos.
L'essentiel du cours est directement inspirŽ du livre de Fulton: "Algebraic
curves". Une partie des exercices proviennent de ce livre, de celui de Hartshorne,

Bernard Le Stum - Courbes AlgŽbriques - Introduction (4/06/99)
"Algebraic geometry" et plus gŽnŽralement des diffŽrent livres d'introduction ˆ la
gŽomŽtrie algŽbrique que j'ai eu l'occasion de consulter. Certains exercices sont
dus ˆ L. Moret-Bailly et P. Berthelot qui m'ont directement prŽcŽdŽ dans l'ensei-
gnement de ce cours.