x g x tan v - + α α 1 . 2 .cos

Pour s’entraîner…..Ch9
Exercice1 : Projeter les vecteurs suivants dans le repère indiqué. Les coordonnées de chaque vecteur seront
indiquées en valeur littérale en fonction de la norme du vecteur et de l’angle 
N°1 N°2 N°3 N°4
Exercice2 :
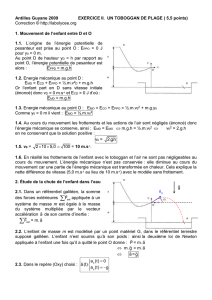
Un enfant glisse le long d’un toboggan de plage dans le référentiel terrestre supposé galiléen.
Pour l’exercice, l’enfant sera assimilé à un point matériel G et on négligera tout type de frottement ainsi que
toutes les actions dues à l’air.
Un toboggan de plage est constitué par :
- une piste DO qui permet à un enfant partant de D sans vitesse initiale d’atteindre le point O avec un
vecteur vitesse
V0
faisant un angle  avec l’horizontale ;
- une piscine de réception : la surface de l’eau se trouve à une distance H au dessous de O.
Étude de la chute de l’enfant dans l’eau à partir du point O :
En O, origine du mouvement dans cette partie, on prendra v0 = 5,0 m.s-1.
1. Énoncer la deuxième loi de Newton.
2. Appliquer la deuxième loi de Newton à l’enfant une fois qu’il a quitté le point O.
3. Déterminer l’expression des composantes ax(t) et ay(t) du vecteur accélération dans le
repère Oxy.
4. Déterminer l’expression des composantes vx(t) et vy(t) du vecteur vitesse dans le repère Oxy.
5. Déterminer l’expression des composantes x(t) et y(t) du vecteur position dans le repère Oxy.
6. Montrer que l’expression de la trajectoire de l’enfant notée y(x) a pour expression :
y(x)=
x
g xtan
v
2
22
0
1.
2 .cos
7. En déduire la valeur de l’abscisse xP du point d’impact P de l’enfant dans l’eau.
Exercice3 :
Une balle est lancée verticalement vers le haut à la vitesse v0 =2 m/s. L’axe Oy est verticale orienté vers le haut
et la balle se trouve en O à l’instant t=0 s.
1. Etablir l’équation horaire de la balle.
2. A quel instant se trouve-elle au sommet de sa trajectoire ?
H
h
D
O
x
y
P
Données :
 Masse de l’enfant : m = 35 kg ;
 Intensité de la pesanteur : g = 10 m.s-2 ;
 Hauteur H = 0,50 m ;
 Angle = 30°

Correction :
Ex1 :
N°1 : Fx=F*cos et Fy =F*sin
 vox= - vocos et voy =vosin
N°3 : vox= vosin et voy = - vocos
N°4 : vox= vocos et voy =- vosin
Exercice2 : Étude de la chute de l’enfant dans l’eau
1. Dans un référentiel galiléen, la somme des
forces extérieures
ext
F
appliquée à un
système de masse m est égale à la masse du
système multipliée par le vecteur accélération
a
de son centre d’inertie :
ext
F
= m.
a
2. L’enfant de masse m est modélisé par un point matériel G, dans le référentiel terrestre supposé
galiléen. L’enfant n’est soumis qu’à son poids : ainsi la deuxième loi de Newton appliquée à l’enfant
une fois qu’il a quitté le point O donne :
P
= m.
a
m.
g
= m.
a
a
=
g
3. Dans le repère (Oxy) choisi :
a
(t)
x
y
a (t) 0
a (t) g
4. Sachant que :
dv
adt
on a :
a
(t)
x
x
y
y
dv
a (t) 0 dt
dv
a (t) g dt
par intégration
v
(t)
x1
y2
v (t) Cte
v (t) g.t Cte
or
0
v
x 1 0
y 2 0
v (0) Cte v .cos
v (0) Cte v .sin
donc
v
(t)
x0
y0
v (t) v .cos
v (t) g.t v .sin
5. Sachant que :
dOG
vdt
on a :
v
(t)
x0
y0
dx
v (t) v .cos dt dy
v (t) g.t v .sin dt
par intégration :
OG
(t)
'
01
2'
02
x(t) v .cos .t Cte
1
y(t) .g.t v .sin .t Cte
2
or
OG
(0)
'
1
'2
x(0) Cte 0
y(0) Cte 0
donc
OG
(t)
0
20
x(t) v .cos .t
1
y(t) .g.t v .sin .t
2
6. On isole le temps t dans x(t) = v0.cos .t et on reporte t dans y(t) pour avoir l’équation de la
trajectoire y(x) :
g
0
v

t =
0
x
v .cos
y(x) =
2
0
00
1 x x
.g. v .sin .
2 v .cos v .cos
y(x)=
2
22
0
1x
.g. x.tan
2 v .cos
2.7. Il faut résoudre l’équation : y(xP) = – H car pour x = xP, y = – H :
donc :
2
PP
22
0
x
1.g. x .tan
2 v .cos
= – H
Calculons les termes devant xP² et xP :
2 2 2 2
0
1 g 1 10
.
2 v .cos 2 5,0 cos (30)
= – 0,27 m-1
tan = tan(30) = 0,58
Il faut résoudre l’équation, avec H = 0,50 m : – 0,27.x²P + 0,58.xP = – 0,50
Soit l’équation du second degré : – 0,27.x²P + 0,58.xP + 0,50 = 0
= (0,58)² – 4 (–0,27) 0,50 = 0,88 et
0,88
= 0,94
les solutions pour xP sont :
P0,58 0,94
x2 0,27
= –0,54 m et
P0,58 0,94
x2 0,27
= 2,8 m
Or xP est positif , xP = 2,8 m
Calculs effectués avec les valeurs non arrondies de tan(30) et de
22
0
1g
.
2 v .cos
D’après correction http://labolycee.org/
Exercice3 : Corrigé rapide
1. 2ème loi de newton
ext
F
= m.
a
d’où
m.= m.
a
soit =
Après projection sur l’axe Oy orienté vers le haut :
ay= - g
Par intégration : vy= - gt + vo
Par inétgration : y= -1/2*g*t²+vo*t
2. Au sommet de la trajectoire : vy= -g*t +vo =0
Soit t =vo/g =2,0/9,8 =0,20 s