Télécharger

Dérivation S 1
Dérivation
Pour reprendre contact n°1 – 2 – 3 – 4 p 73
I. Nombre dérivé et tangente
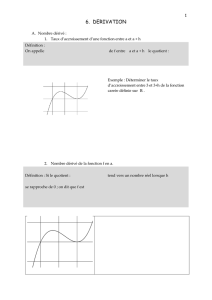
A. Taux d’accroissement
Définition
 est une fonction définie sur un intervalle  ;  et    sont deux nombres réels de  avec   .
Le taux d’accroissement de  entre  et    est le rapport 
B. Nombre dérivé d’une fonction en un point
Définition
 est une fonction définie sur un intervalle  ;  et    sont deux nombres réels de  avec   .
Dire que  est dérivable en  signifie que lorsque  tend vers , le taux d’accroissement 
 tend
vers un réel , ce que l’on note
est appelé le nombre dérivé de en  et on le note 
Notation
se lit limite de 
 quand h tend vers 0.
Exercice résolu n°1 p 77
Exercices n°20 à 24 p 88 – 89
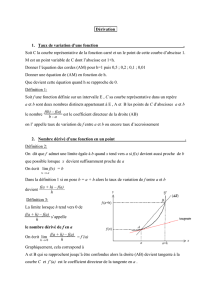
C. Tangente à la courbe représentative d’une fonction
Interprétation graphique
Définition
Soit  une fonction dérivable en ,  sa courbe représentative et  le point de  d’abscisse .
La tangente à la courbe  au point  est la droite passant par  et dont le coefficient directeur est .

Dérivation S 2
Propriété
Soit  une fonction dérivable en ,  sa courbe représentative et  le point de  d’abscisse .
La tangente à la courbe  au point  a pour équation :       
Démonstration (voir p 76)
La tangente T à  en  a une équation de la forme     .
   appartient à T donc     . D’où     
Donc on a         
Exercice résolu n°2 p 77
Exercices n°25 à 35 p 89 - 90
D. Fonction dérivée
Définition
 est une fonction définie sur un intervalle 
Dire que est dérivable sur  signifie que  est dérivable en tout nombre réel de .
La fonction dérivée de  est la fonction qui, à tout nombre réel  de I, associe 
Elle est définie sur  par     
Remarque
Dans l’écriture de la fonction, le nom de la variable n’a pas d’importance, on peut autant écrire :
𝑓 𝑎  𝑓𝑎 𝑓 𝑡  𝑓𝑡 𝑓 𝑥  𝑓𝑥
Le nom est souvent choisi d’après le contexte, la variable t représente en général le temps.
Exercices n°36 – 37 p 90
II. Dérivées des fonctions usuelles
A. Fonctions constantes    avec   R
Propriété
 est la fonction définie sur R par   
 est dérivable sur R et, pour tout nombre réel,   
Démonstration
Pour tous nombres réels  et   , on a 
  qui tend vers 0 quand  tend vers 0.
Donc  est dérivable en tout réel  et   
B. Fonctions identité
Propriété
 est la fonction définie sur R par   
 est dérivable sur  et, pour tout nombre réel,   
Démonstration
Pour tous nombres réels  et   , on a 
  qui tend vers 1 quand  tend vers 0.
Donc  est dérivable en tout réel  et   

Dérivation S 3
C. Fonctions carré
Propriété
 est la fonction définie sur R par   
 est dérivable sur  et, pour tout nombre réel,   
Démonstration
Pour tous nombres réels  et   , on a 
   qui tend vers  quand 
tend vers 0. Donc  est dérivable en tout réel  et   
D. Fonctions carré
Propriété
 est la fonction définie sur R par   
 est dérivable sur  et, pour tout nombre réel,   
Démonstration
Pour tous nombres réels  et   , on a 
     qui tend vers  quand  tend vers 0.
Donc  est dérivable en tout réel  et   
E. Fonctions puissances   avec  entier,   
Propriété (admise)
 est la fonction définie sur R par   
 est dérivable sur  et, pour tout nombre réel,   
F. Fonctions inverse
Propriété
 est la fonction définie sur      par   
 est dérivable sur      et, pour tout nombre réel,   
Démonstration
Pour tous nombres réels    et    et     , on a
 qui tend vers 
 quand  tend vers 0.
Donc  est dérivable en tout réel  R* et    
G. Fonctions racine carrée
Propriété
 est la fonction définie sur   par   
 est dérivable sur   et, pour tout nombre réel, 
Démonstration
Pour tous nombres réels  et    et     , on a
 qui tend vers 
 quand  tend vers 0.
Donc  est dérivable en tout réel    et   
Exercices n°38 – 39 – 40 – 41 – 42 – 43 p 90 – 91

Dérivation S 4
III. Dérivées et opérations sur les fonctions
A. Somme de fonctions et produit par un réel
Propriété
Si      avec  et  dérivables sur  alors  est dérivable sur  et     
Démonstration (voir p 80)
Pour tout  de , on a 
Or  et  sont dérivables en , donc 
 tend vers  quand  tend vers 0 et   tend vers  quand  tend
vers 0
Donc 
 tend vers   quand  tend vers 0
Donc  est dérivable en tout réel    et   
Propriété
Si    avec  dérivable sur  alors  est dérivable sur  et  
Démonstration (voir p 80)
Pour tout  de , on a 
Or  est dérivable en , donc 
 tend vers  quand  tend vers 0
Donc 
 tend vers
 quand  tend vers 0
Donc  est dérivable en tout réel    et 
Définition et Propriété
Une fonction  définie sur R est une fonction polynôme si  peut s’écrire comme la somme de termes
de la forme   N et  constante réelle.
Toutes les fonctions polynômes sont dérivables sur R
Démonstration
C’est une conséquence des deux propriétés précédentes.
Exercices n°45 à 48 p 91
B. Produit, inverse et quotient de fonctions
Propriété
Si    avec  et  dérivables sur  alors  est dérivable sur  et
Démonstration (voir p 82) à connaître
Pour tout  de , on a 
On ajoute et on retranche    pour faire apparaître les quotients 
 et 
Si on admet que    tend vers  quand  tend vers 0, 
 tend vers   
Donc  est dérivable en  et     
Remarque : Si 𝒗𝒙  (constante), alors 𝒗𝒂  𝟎et on retrouve 𝒇𝒂  𝒖𝒂
Exercice n°49 p 91

Dérivation S 5
Propriété
Si   
 avec  dérivable sur  et si   , alors  est dérivable sur  et   
Si   
 avec  et  dérivables sur  et si   alors  est dérivable sur  et
Démonstration
Exercice n°95 p 96
Exercices n°50 – 51 p 91
Définition et Propriété
Toutes les fonctions de la forme   
 où u et v sont des fonctions polynômes s’appellent des fonctions
rationnelles.
Toute fonction rationnelle est dérivable sur son ensemble de définition.
Démonstration
C’est une conséquence des deux propriétés précédentes.
Exercices n°52 – 53 – 54 p 91
Exercices n°56 – 57 – 58 – 59 – 60 p 92 – 93
Exercices n°66 - 67 p 93
DM n°96 – 97 p 96 – 97