LES FONCTIONS DE REFERENCE

LES FONCTIONS DE REFERENCE
I. Les fonctions affines :
Définition : On appelle fonction affine toute fonction définie sur IR , ou sur un intervalle de IR , par
f : x  ax + b avec a et b deux nombres réels.
Propriétés :
La représentation graphique d'une fonction affine est une droite d'équation y = ax + b.
Le coefficient directeur est a et l'ordonnée à l'origine est b.
Le vecteur directeur est u ( 1 ; a ).
Si a > 0 la fonction est croissante .
Si a = 0 la fonction est constante. La courbe représentative est une droite parallèle à l'axe des abscisses.
Si a < 0 la fonction est décroissante.
Tableau de variation :
Si a > 0
Si a < 0
–
x
f(x)
b
a
x
0
f(x)
–
b
a
0
b
b
. Le point de coordonnées ( – ; 0 ) est le
a
a
point d'intersection de la courbe représentative de f avec l'axe des abscisses.
Remarques : f(x) = 0 si ax + b = 0 c'est-à dire si x = –
Si x = 0 f ( 0 ) = b. Le point de coordonnées ( 0 , b ) est le point intersection de la droite
représentative de la fonction f avec l'axe des ordonnées.
Représentation graphique :
Si a > 0
Si a = 0
Si a < 0
b
b
0
0
-
0
b
a
-
b
a
b
Si b = 0 la fonction est dite linéaire. Sa courbe représentative est une droite passant par l'origine du repère.
Exemple : Représenter dans un même repère les quatre fonction suivantes :
f(x) = 10x – 2 ; g(x) = – 8x + 4 ; h(x) = 7x ; l(x) = – 3
1ère STI Ch 1 Les fonctions de référence 2010–2011 F.Tournier
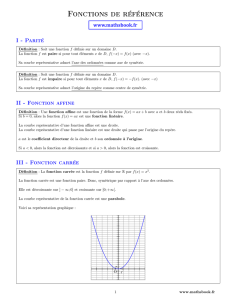
II. La fonction carrée :
C'est la fonction définie par : f : x  x² .
Elle est définie sur R.
Elle est paire car f( – x) = f(x) .
Sa représentation graphique est symétrique par rapport à l'axe des ordonnées.
Elle passe par l'origine , c'est une parabole.
La fonction f est décroissante pour x négatif et croissante pour x positif.
Tableau de variation :
x
Courbe représentative :
0
f(x)
0
0
III. La fonction cube :
C'est la fonction définie par : f : x  x3 .
Elle est définie sur R.
Elle est impaire car f( – x) = – f(x) .
Sa représentation graphique est symétrique par rapport à l'origine.
Elle passe par l'origine .
La fonction f est croissante pour tout x .
Tableau de variation :
Courbe représentative :
x
0
f(x)
0
0
1ère STI Ch 1 Les fonctions de référence 2010–2011 F.Tournier
3
IV. La fonction inverse :
1
C'est la fonction définie par : f : x  .
x
Elle n'est pas définie en 0. Son ensemble de définition est ] –
;0[
]0;+
[.
Elle est impaire car f( – x) = – f(x) .
Sa représentation graphique est symétrique par rapport à l'origine .
C'est une hyperbole.
La fonction f est décroissante sur les deux intervalles de son domaine de définition..
Tableau de variation :
x
Courbe représentative :
0
f(x)
La double barre dans le tableau de variation
indique que la fonction n'est pas définie
pour la valeur 0.
0
V. La fonction racine carrée :
C'est la fonction définie par : f : x  x .
Elle n'est définie que pour des nombres positifs. Son ensemble de définition est [ 0 ; +
[.
Elle n'est ni paire ni impaire car son ensemble de définition n'est pas symétrique par rapport à 0. .
Sa représentation graphique passe par l'origine .
La fonction f est croissante sur son domaine de définition.
Tableau de variation :
x
Courbe représentative :
0
f(x)
0
0
1ère STI Ch 1 Les fonctions de référence 2010–2011 F.Tournier
4
VI. Les fonctions trigonométriques :
1) La fonction cosinus : f(x) = cos(x)
Son ensemble de définition est IR .
Pour tout x de IR on a : – 1
cos(x)
1
Rappel sur le cercle trigonométrique :
Tableau de valeurs :
x
en radians
cos x
–
–1
–
2
0
–
3
1
2
–
4
2
2
–
6
3
2
0
1
6
3
2
Représentation graphique :
1ère STI Ch 1 Les fonctions de référence 2010–2011 F.Tournier
4
2
2
3
1
2
2
0
–1
5
Propriétés importantes :
a) La fonction cosinus est 2 – périodique c'est–à–dire que cos(x) = cos( x + 2 ) = cos ( x – 2
Pour tout réel x on a cos(x) = cos( x + 2 k ) avec k ZZ ( entiers relatifs ).
)…
b) La fonction cosinus est paire . En effet pour tout réel x , cos( x ) = cos( – x )
Sa représentation graphique est donc symétrique par rapport à l'axe des abscisses.
2) La fonction sinus : f(x) = sin(x)
Son ensemble de définition est IR .
Pour tout x de IR on a : – 1
sin(x)
1
Tableau de valeurs :
x
en radians
sin x
–
0
–
2
–1
–
3
3
–
2
–
4
2
–
2
–
6
1
–
2
0
0
6
1
2
4
2
2
3
3
2
2
1
0
Représentation graphique :
Propriétés importantes :
a) La fonction sinus est 2 – périodique c'est–à–dire que sin(x) = sin( x + 2 ) = sin( x – 2
Pour tout réel x on a sin(x) = sin( x + 2 k ) avec k ZZ ( entiers relatifs ).
b) La fonction sinus est impaire . En effet pour tout réel x , sin( x ) = – sin( – x )
Sa représentation graphique est donc symétrique par rapport à l'origine du repère.
1ère STI Ch 1 Les fonctions de référence 2010–2011 F.Tournier
)…