DS5 fonctions linéaire et affine 2013

3
ème
B DS5 fonctions linéaire et affine 2013-2014 sujet 1
1
3x
3
2
2,5
Exercice 1 (12 points)
Les droites (DC) et (BE) sont
parallèles.
a) Démontrer que la fonction qui à
x associe DC est une fonction
linéaire.
b) Démontrer que la fonction qui à
x associe BC est une fonction
affine.
c) Dans un repère, représenter les
fonctions f et g telles que
f(x) = 2x et g(x) = 3x – 3.
d) Lire sur le graphique, l’abscisse du point d’intersection des deux droites.
Pour cette valeur de x, quelle est la nature du triangle BDC ?
Exercice 2 (8 points)
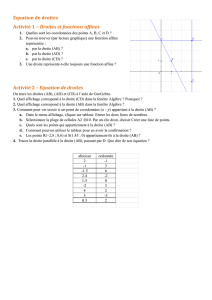
On a représenté les fonctions f et g dans un repère.
a) Pour quelle valeur de x a-t-on f(x) = g(x) ?
b) Déterminer les expressions algébriques de f et g.
c) En utilisant les expressions trouvées précédemment, retrouver par le calcul les
résultats de la question a).

3
ème
B DS5 fonctions linéaire et affine 2013-2014 sujet 2
2
2
2x
1
2
Exercice 1 (12 points)
Les droites (AC) et (ED) sont parallèles.
a) Démontrer que la fonction qui à x
associe AC est une fonction
linéaire.
b) Démontrer que la fonction qui à x
associe CD est une fonction
affine.
c) Dans un repère, représenter les
fonctions f et g telles que
f(x) = x et g(x) = 2x – 2.
d) Lire sur le graphique, l’abscisse du
point d’intersection des deux droites.
Pour cette valeur de x, quelle est la nature du triangle ACD ?
Exercice 2 (8 points)
On a représenté les fonctions f et g dans un repère.
a) Pour quelle valeur de x a-t-on f(x) = g(x) ?
b) Déterminer les expressions algébriques de f et g.
c) En utilisant les expressions trouvées précédemment, retrouver par le calcul les
résultats de la question a).

3
ème
B DS5 fonctions linéaire et affine 2013-2014 sujet 1
CORRECTION
3
3x
3
2
2,5
Exercice 1 (13 points)
Les droites (DC) et (BE) sont parallèles.
a) Démontrer que la fonction qui à x associe
DC est une fonction linéaire.
b) Démontrer que la fonction qui à x associe
BC est une fonction affine.
c) Dans un repère, représenter les fonctions f
et g telles que
f(x) = 2x et g(x) = 3x – 3.
d) Lire sur le graphique, l’abscisse du point
d’intersection des deux droites.
Pour cette valeur de x, quelle est la nature du triangle BDC ?
a) Les droites (DC) et (BE) étant parallèles, on peut appliquer le théorème de Thalès dans les
triangles ABE et ACD :
AB
AC = AE AD = BE DC
Soit 3
3x = 2 DC
D’où : 3×DC = 3x×2
Soit : DC = 2x
La fonction qui à x associe la longueur DC est : x  2x.
Il s’agit bien d’une fonction linéaire (de coefficient 2).
b) BC = AC – AB = 3x – 3.
La fonction qui à x associe la longueur BC est : x  3x – 3.
Il s’agit bien d’une fonction affine (de la forme ax + b avec a = 3 et b = -3).
c)
d) L’abscisse du point d’intersection des deux droites est 3.
Pour x = 3, BC = 3×3 – 3 = 6
DC = 2×3 = 6.
BC = DC, donc le triangle BDC est isocèle en C.
(On ne sait pas s’il est de plus équilatéral : il faudrait calculer BD).

3
ème
B DS5 fonctions linéaire et affine 2013-2014 sujet 1
CORRECTION
4
Exercice 2 (8 points)
On a représenté les fonctions f et g dans un repère.
a) Pour quelle valeur de x a-t-on f(x) = g(x) ?
b) Déterminer les expressions algébriques de f et g.
c) En utilisant les expressions trouvées précédemment, retrouver par le calcul les résultats de
la question a).
a) f(x) = g(x) pour x = 3 (abscisse du point d’intersection des deux droites)
b) La représentation graphique de la fonction f est une droite.
Donc f est une fonction affine.
f(x) = ax + b
f(0) = 1 ; donc b = 1
f(1) = 2 donc a×1 + 1 = 2
Soit a = 2 – 1 = 1
Donc f(x) = x + 1
La représentation graphique de la fonction g est une droite.
Donc g est une fonction affine.
g(x) = ax + b
g(0) = 5 donc b = 5
g(3) = 4 donc a×3 + 5 = 4
Soit a = 4 – 5
3 = - 1 3
Soit g(x) = - 1
3x + 5
c) On résout l’équation f(x) = g(x)
x + 1 = - 1
3x + 5
Soit x + 1
3x = 5 - 1
Soit 4
3x = 4
Soit x = 4×3
4 = 3

3
ème
B DS5 fonctions linéaire et affine 2013-2014 sujet 2
CORRECTION
5
2
2x
1
2
Exercice 1 (12 points)
Les droites (AC) et (ED) sont parallèles.
a) Démontrer que la fonction qui à x
associe AC est une fonction linéaire.
b) Démontrer que la fonction qui à x
associe CD est une fonction affine.
c) Dans un repère, représenter les
fonctions f et g telles que
f(x) = x et g(x) = 2x – 2.
d) Lire sur le graphique, l’abscisse du
point d’intersection des deux droites.
Pour cette valeur de x, quelle est la
nature du triangle ACD ?
a) Les droites (AC) et (ED) étant parallèles, on peut appliquer le théorème de Thalès dans les
triangles BDE et BCA :
BD
BC = DE CA = BE BA
Soit : 2
2x = 1 AC = 2 BA
On en déduit que AC = x.
La fonction qui à x associe la longueur AC est : x  x.
Il s’agit bien d’une fonction linéaire (de coefficient 1).
b) CD = BC – BD = 2x - 2
La fonction qui à x associe la longueur CD est : x  2x – 2.
Il s’agit bien d’une fonction affine (de la forme ax + b avec a = 2 et b = -2).
c)
c) L’abscisse du point d’intersection des deux droites est 2.
Pour x = 2, AC = 2
DC = 2×2 – 2 = 2.
AC = DC, donc le triangle ACD est isocèle en C.
(On ne sait pas s’il est de plus équilatéral : il faudrait calculer AD).