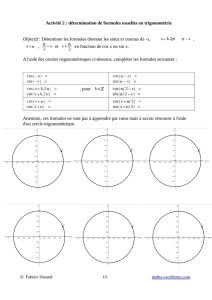
TS5 Test dérivées (sujet A) Pour chaque fonction, déterminer son

TS5
Test dérivées (sujet A)
Pour chaque fonction, déterminer son domaine de définition, et calculer sa
fonction dérivée f’. (écrire les formules et étapes de calcul)
f(x) = 3
√
4x2+6x−4
f(x) = ( cosx )5
f(x) =
4
(2x−3)7
f(x) = sin (2 – 3x)
TS5
Test dérivées (sujet A)
Pour chaque fonction, déterminer son domaine de définition, et calculer sa
fonction dérivée f’. (écrire les formules et étapes de calcul)
f(x) = 3
√
4x2+6x−4
f(x) = ( cosx )5
f(x) =
4
(2x−3)7
f(x) = sin (2 – 3x)
TS5
Test dérivées (sujet B)
Pour chaque fonction, déterminer son domaine de définition, et calculer sa
fonction dérivée f’. (écrire les formules et étapes de calcul)
f(x) = cos (4x – 3)
f(x) = 5
√
4x2−7x−2
f(x) = ( sin x )6
f(x) =
−3
(5x+1)4
TS5
Test dérivées (sujet B)
Pour chaque fonction, déterminer son domaine de définition, et calculer sa
fonction dérivée f’. (écrire les formules et étapes de calcul)
f(x) = cos (4x – 3)
f(x) = 5
√
4x2−7x−2
f(x) = ( sin x )6
f(x) =
−3
(5x+1)4

Correction sujet A
f(x) = 3
√
4x2+6x−4
DfIl faut que 4x2 + 6x – 4  0  = b2 – 4 ac = 36+ 64 = 100 > 0
donc 2 racines réelles :
x1=−6−
√
100
8=−16 8=−2
et
x2=−6+
√
100
8=4 8=1 2=0,5
4x2 + 6x – 4 est du signe de a = 4 > 0 à l’extérieur de ses racines,
donc Df = ]-  ; -2]  [0,5 ; +  [
f est de la forme 3
√
u
avec u(x) = 4x2 + 6x – 4 et u’(x) = 8x + 6.
f ’ =
3u '
2
√
u
, donc f ’(x) = 3
8x+6
2
√
4x2+6x−4
= 3
4x+3
√
4x2+6x−4
=
12 x+9
√
4x2+6x−4
f(x) = ( cosx )5Pas de contrainte, donc Df = IR.
f est de la forme u5 avec u(x) = cos x et u’(x) = - sin x.
f ’ = 5 u’ u4, donc f ’(x) = - 5 sinx (cos x )4.
f(x) =
4
(2x−3)7
DfIl ne faut pas que 2x – 3 = 0  x = 1,5
Df = IR \ {1,5}
f est de la forme
4
u7
= 4 u-7 avec u(x) = 2x – 3 et u’(x) = 2
f ’ = 4  (-7) u’ u-8, donc f ’(x) = - 28  2 ( 2x – 3)-8 =
−56
(2x−3)8
f(x) = sin (2 – 3x) Pas de contrainte, donc Df = IR.
f est de la forme sin (ax + b) avec sin’ = cos ; a = -3 et b = 2.
f ’(x) = a cos (ax + b) = -3 cos (2 – 3x)
Correction sujet B
f(x) = cos (4x – 3) Pas de contrainte, donc Df = IR.
f est de la forme cos (ax + b) avec cos’ = - sin ; a = 4 et b = -3.
f ’(x) = - a sin (ax + b) = -4 sin (4x – 3)
f(x) = 5
√
4x2−7x−2
DfIl faut que 4x2 – 7x – 2  0  = b2 – 4 ac = 49 + 32 = 81 > 0
donc 2 racines réelles :
x1=7−
√
81
8=−2 8=−1 4
et
x2=7+
√
81
8=16 8=2
4x2 – 7x – 2 est du signe de a = 4 > 0 à l’extérieur de ses racines,
donc Df = ]-  ; -0,25  [2 ; +  [
f est de la forme 5
√
u
avec u(x) = 4x2 – 7x – 2 et u’(x) = 8x – 7 .
f ’ =
5u '
2
√
u
, donc f ’(x) = 5
8x−7
2
√
4x2−7x−2
=
40 x−35
2
√
4x2−7x−2
f(x) = ( sin x )6Pas de contrainte, donc Df = IR.
f est de la forme u6 avec u(x) = sin x et u’(x) = cos x.
f ’ = 6 u’ u5, donc f ’(x) = 6 cos x (sin x )5.
f(x) =
−3
(5x+1)4
DfIl ne faut pas que 5x + 1 = 0  x = -0,2
Df = IR \ {- 0,2}
f est de la forme
−3
u4
= -3 u-4 avec u(x) = 5x + 1 et u’(x) = 5
f ’ = -3  (-4) u’ u-5, donc f ’(x) = 12  5 ( 5x + 1)-5 =
60
(5x+1)5