Limites – Comportement asymptotique

Limites – Comportement asymptotique
Christophe ROSSIGNOL∗
Année scolaire 2009/2010
Table des matières
1 Limite d’une fonction en +∞, en −∞ 3
1.1 Limite infinie en +∞, en −∞ ...................................... 3
1.2 Limite finie en +∞, en −∞ – Asymptote horizontale . . . . . . . . . . . . . . . . . . . . . . . . . 5
2 Limite en un réel a7
2.1 Deuxexemplesdebase.......................................... 7
2.2 Limite infinie en un réel a–Asymptoteverticale ........................... 7
2.3 Casdesfonctionsusuelles ........................................ 8
3 Opérations sur les limites 8
3.1 Positionduproblème........................................... 8
3.2 Sommededeuxfonctions ........................................ 8
3.3 Produitdedeuxfonctions ........................................ 9
3.4 Inversed’unefonction .......................................... 9
3.5 Quotientdedeuxfonctions ....................................... 10
4 Limite en l’infini d’une fonction polynôme ou rationnelle 12
4.1 Casd’unefonctionpolynôme ...................................... 12
4.2 Casd’unefonctionrationnelle...................................... 12
5 Asymptote oblique 13
∗Ce cours est placé sous licence Creative Commons BY-SA http://creativecommons.org/licenses/by-sa/2.0/fr/
1

TABLE DES FIGURES LISTE DES TABLEAUX
Table des figures
1 Limite +∞lorsque xtend vers +∞.................................. 3
2 Fonctionracinecarrée .......................................... 4
3 Fonctionidentité ............................................. 4
4 Fonctioncarrée.............................................. 4
5 Fonctioncube............................................... 4
6 Limite finie lorsque xtend vers +∞.................................. 5
7 Fonction x→1
√x............................................. 6
8 Fonctioninverse ............................................. 6
9 Fonction x−→ 1
x2............................................ 6
10 Asymptoteoblique ............................................ 13
Liste des tableaux
1 Limited’unesomme ........................................... 8
2 Limited’unproduit ........................................... 9
3 Limitedel’inverse ............................................ 10
4 Limited’unquotient........................................... 11
2

1 LIMITE D’UNE FONCTION EN +∞, EN −∞
Activité : Activité 1 page 112 [TransMath]
1 Limite d’une fonction en +∞, en −∞
1.1 Limite infinie en +∞, en −∞
Définition : Soit fune fonction définie sur l’intervalle [α; +∞[.
Dire que ftend vers +∞lorsque xtend vers +∞signifie que l’on peut rendre les valeurs de f(x)
aussi grandes que l’on veut dès que xest suffisamment grand.
On note alors :
lim
x→+∞
f(x)=+∞ou lim
+∞
f= +∞
Remarques :
1. On dit aussi que fa comme limite +∞en +∞.
2. Ceci peut se traduire par :
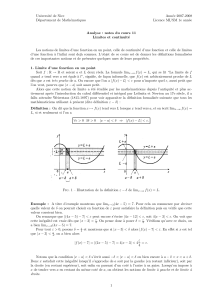
pour tout réel A > 0, il existe un réel a > 0tel que f(x)> A dès que x>a(voir figure 1)
Fig. 1 – Limite +∞lorsque xtend vers +∞
3. On peut définir de manière analogue limx→+∞f(x) = −∞;limx→−∞ f(x)=+∞et limx→−∞ f(x) =
−∞.
Cas des fonctions usuelles :
– Fonction racine carrée (figure 2) :
lim
x→+∞
√x= +∞
– Fonction identité (figure 3) :
lim
x→−∞
x=−∞ et lim
x→+∞
x= +∞
– Fonction carrée (figure 4) :
lim
x→−∞
x2= +∞et lim
x→+∞
x2= +∞
– Fonction cube (figure 5) :
lim
x→−∞
x3=−∞ et lim
x→+∞
x3= +∞
Remarque : On peut montrer que, si nentier strictement positif :
– Si nest pair :limx→−∞ xn= +∞et limx→+∞xn= +∞
– Si nest impair :limx→−∞ xn=−∞ et limx→+∞xn= +∞
3

1.1 Limite infinie en +∞, en −∞ 1 LIMITE D’UNE FONCTION EN +∞, EN −∞
Fig. 2 – Fonction racine carrée
Fig. 3 – Fonction identité
Fig. 4 – Fonction carrée
Fig. 5 – Fonction cube
4

1 LIMITE D’UNE FONCTION EN +∞, EN −∞ 1.2 Limite finie en +∞, en −∞ – Asymptote horizontale
1.2 Limite finie en +∞, en −∞ – Asymptote horizontale
Définition : Soit fune fonction définie sur l’intervalle [α; +∞[et lun nombre réel.
Dire que ftend vers llorsque xtend vers +∞signifie que l’on peut rendre les valeurs de f(x)aussi
proches de lque l’on veut dès que xest suffisamment grand.
On note alors :
lim
x→+∞
f(x) = lou lim
+∞
f=l
Remarques :
1. On dit aussi que fa comme limite len +∞.
2. Ceci peut se traduire par :
pour tout réel α > 0(αaussi proche de zéro que possible), il existe un réel a > 0tel que
l−α < f (x)< l +αdès que x>a(voir figure 6)
Fig. 6 – Limite finie lorsque xtend vers +∞
3. On peut définir de manière analogue limx→−∞ f(x) = l.
Cas des fonctions usuelles :
– Fonction x−→ 1
√x(figure 7) :
lim
x→+∞
1
√x= 0
– Fonction inverse (figure 8) :
lim
x→−∞
1
x= 0 et lim
x→+∞
1
x= 0
– Fonction x−→ 1
x2(figure 9) :
lim
x→−∞
1
x2= 0 et lim
x→+∞
1
x2= 0
Remarque : On peut montrer que, si nentier strictement positif : limx→−∞ 1
xn= 0 et limx→+∞1 xn= 0.
Définition : Lorsque limx→+∞f(x) = l(respectivement limx→−∞ f(x) = l), on dit que la droite d’équation
y=lest asymptote (horizontale) à la courbe représentant f.
Remarque : Graphiquement, ceci signifie que la courbe représentant fse rapproche de plus en plus de cette
droite lorsque xdevient grand1(voir figure 6).
1éventuellement négatif et grand en valeur absolue pour l’asymptote en −∞.
5