NOMBRES RÉELS ET LIMITES Définition 1. On dira qu`un nombre a

NOMBRES RÉELS ET LIMITES
Définition 1. On dira qu’un nombre aest réel si apeut être approché arbitrairement
près par des nombres rationnels (ou décimaux). L’ensemble des nombres réels se note
R. Une propriété spécifique de Rest d’être un ensemble complet (intuitivement "sans
trous"), c’est-à-dire que tout ensemble borné admet un supremum 1appartenant à R.
Cette propriété n’est pas vérifiée par Q: prendre A={x∈Q|x2<2}alors sup(A)6∈ Q.
Définition 2. Un concept (topologique) fondamental en analyse, attaché à la droite réelle
R, est celui de voisinage d’un point a∈R(fixé). Pour simplifier les choses, on dira que tout
intervalle ouvert Uacontenant le point aest un voisinage de a. Il importe de s’imaginer
que le point aest comme "englouti" dans un intervalle ouvert, ce dernier pouvant être
rendu arbitrairement "petit", mais dans tous les cas Uane peut être réduit au point a. Il
est habituel de choisir comme voisinage "standard" d’un point aappartenant à l’axe des
abscisses
Ua={x∈R;|x−a|< δ}(pour un δ > 0que l’on se fixe)
En français cela donne : Uaest l’ensemble des nombres réels xtels que la distance de xàa
est inférieure à δ. Dans ce cas Uaest un intervalle centré autour de ade longueur 2δ. Si b
appartient à l’axe des ordonnées alors un voisinage standard est Vb={y∈R;|y−b|< }
pour un  > 0que l’on se fixe.
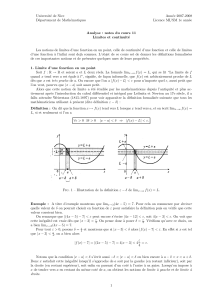
Définition 3. Formellement dire que la "limite lorsque xtend vers ade f(x)existe et
égale à b", que l’on dénote par limx→af(x) = b, signifie que quel que soit le voisinage
Vbde b(aussi petit que l’on veut) il existe un voisinage Uade atel que pour tous les x
compris dans Ua(mais x6=a) on a toujours f(x)∈Vb. Avec des notations mathématiques
cela donne :
lim
x→af(x) = b⇔ ∀Vb∃Ua;∀x∈Uax6=a f(x)∈Vb
où Uaet Vbreprésentent des voisinages de aet brespectivement
En utilisant les voisinages standard ci-dessus cela donne :
lim
x→af(x) = b⇔ ∀ > 0∃δ > 0; si |x−a|< δ (mais x6=a)alors |f(x)−b|< 
que l’on peut traduire par : "pour tout voisinage (centré) de bde longueur 2, il existe
un voisinage (centré) de ade longueur 2δtels que, si xappartient à ce dernier voisinage
(mais x6=a) alors f(x)appartient au voisinage autour de b".
C’est seulement à partir d’une telle définition que l’on peut démontrer des propriétés
telles que l’unicité de la limite (si elle existe) et les résultats essentiels suivants :
Théorème 1. Si limx→af(x) = met limx→ag(x) = nalors
a) la limite de la somme égale la somme des limites : limx→a(f+g)(x) = m+n
b) la limite du produit égale le produit des limites : limx→a(f·g)(x) = m·n
c) la limite du quotient égale le quotient des limites : limx→a(f
g)(x) = m nsi n6= 0
Par ailleurs si limy→mg(y) = nalors la compostion g◦fadmet une limite en aet
limx→a(g◦f)(x) = névidemment !
Remarque. Bien qu’implicite dans le développement de l’Analyse au 17eet 18esiècle, la
notion morderne de limite d’une fonction remonte à Bolzano, qui en 1817 a introduit la
base des δet pour définir la continuité d’une fonction. L’on doit la définition formelle
d’une limite d’abord à Cauchy dans son Cours d’Analyse (1821) et surtout à Weierstrass
(∼1870).(cf. Wikipedia)
C. Aebi, Collège Calvin, Genève, Suisse
1. Plus petit élément plus grand que tous les autres de l’ensemble en question
1