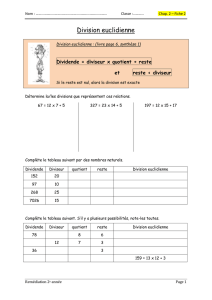
Quel est le plus petit nombre à ajouter au dividende pour que le

Quel est le plus petit nombre à ajouter au dividende
pour que le quotient de la division euclidienne de 65 par 8 augmente de 2 ?
Résolution:
65=8*8+1
Pour que le quotient augmente de 2, il faut ajouter au minimum 15 = (8-1)+8
Contrôle : 65+15=80
80=8*10+0 ok !!!
Quel est le plus grand nombre à retrancher au dividende
pour que le quotient de la division euclidienne de 245 par 13 diminue de 1 ?
Résolution:
245=13*18+11
Pour que le quotient diminue de 1, il faut anuller le reste et enlever un de plus.
Il faut donc enlever 11+1=12 au dividende pour que le quotient diminue de 1.
Contrôle: 245-12=233 233=13*17+12 ok!!!
Le sujet de la phrase : en rouge
Le verbe relatif au sujet : souligné
L’apposition : en vert
La question (toujours pareille) se compose d’une première partie Question et d’une
deuxième partie de calcul effectif.
Quel est le plus petit nombre à ajouter au dividende
pour que le quotient de la division euclidienne de 547 par 23 augmente de 7 ?
Explication :
547=23*23+18 quotient
Pour que le quotient augmente de 1, il faut ajouter au minimum (23-18)=5 +1
Pour qu’il augmente encore une fois de 1, il faut encore augmenter de b=23 +1
En tout il augmente de 7 = 1+6.
Donc il faut ajouter 5 (une première fois) +6*23=5+6*23=5+138=143
Il faut donc ajouter au minimum 143 pour que …
Alternative : J’ajoute 7*23 pour que le quotient augmente certainement de 7 et j’enlève
ensuite le reste du début r=18 : 7*23-18=161-18=143