Triangles rectangles

1/3
TRIGONOMETRIE
1) Cosinus et sinus
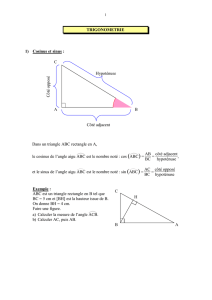
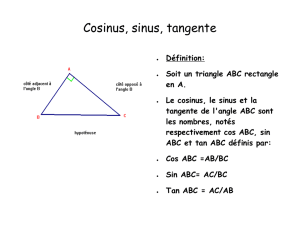
Dans un triangle ABC rectangle en A,
le cosinus de l’angle aigu
ABC
est le nombre not• : cos
ABC
=
AB
BC
=
cÄtÅ adjacent
hypotÅnuse
,
et le sinus de l’angle aigu
ABC
est le nombre not• : sin
ABC
=
AC
BC
=
cÄtÅ opposÅ
hypotÅnuse
Exemple :
ABC est un triangle rectangle en B tel que
BC = 5 cm et [BH] est la hauteur issue de B.
On donne BH = 4 cm.
Faire une figure.
a) Calculer la mesure de l’angle
ACB
.
b) Calculer AC, puis AB.
CÄtÅ adjacent
A B
C
HypotÅnuse
CÄtÅ opposÅ
AB
C
H

2/3
2) Tangente
Dans un triangle ABC rectangle en A,
la tangente de l’angle aigu
ABC
est le nombre not• :
AC
tan ABC AB
cÄtÅ opposÅ
cÄtÅ adjacent
Remarque :
Le cercle a pour rayon OJ = OA = 1 et (AB) est tangente au cercle en A.
Alors
HB 4 4
tan HCB 63 = HA B
HC 2tan 27
A+C 90
.
Exemple :
BH = 4 cm et CH = 2 cm.
a) Calculer la mesure de l’angle
ACB
.
ACB HCB
. Dans le triangle HCB rectangle en H,
HB 4
tan HCB =
HC 2
. Donc
HCB 63
.
b) Calculer AH.
Dans le triangle ABC rectangle en B,
A+C 90
.
Donc
A 90 63
, donc
A 27
.
Dans le triangle HAB rectangle en H,
HB
tan HAB
HA
, donc
4
tan 27
HA
  .
Donc HA xtan 27‚ 4. Donc
4
HA
tan 27
7,9 cm.
3) Formules de trigonomÄtrie
sin 2x+ cos 2x= 1
sin
tan
cos
x
x
x
cos x= sin (90‚ – x) sin x= cos (90‚ – x)
Exemple:Construire un triangle ABCrectangle en A tel que
1
sin ABC
2
.
Calculer ensuite
cos ABC
, puis
tan ABC
.
sin 2x+ cos 2x= 1, donc
sin ÇABC cos ÇABC 1
.
Donc
2
1
cos ÇABC 1
2
  , d’o„
2
1
cos ÇABC 1
2
. Donc
2
1 1
cos ABC 1 1
2 4
  ,
Car le cosinus d’un angle aigu est toujours positif.
Donc
3 3
cos ABC 4
4
  . Finalement
3
cos ABC
2
.
Donc
1
sin ABC 1 2
2
tan ABC 2
3 3
cos ABC
2
    . Donc
1 3
tan ABC
3
3
  .
A B
C
OA
B
J
I
x
AB
C
H
4
cm
2
cm
63Ä
27
‚
7,9
cm
1
2
A
B
C

3/3
4) Tableau des valeurs particuliÅres
sin cos tan
0‚ 0 1 0
30‚
1
2
3
2
1 3
3
3
45‚
2
2
2
2
1
60‚
3
2
1
2
3
90‚ 1 0