Aspect énergétique de la mécanique du point

I Travail d’une force. Théorème de l’énergie cinétique
A) Puissance – travail élémentaire
On considère un référentiel (R) et un point matériel, soumis à une force
F
, qui se
déplace de M à M’ infiniment voisins. Travail de
F
sur ce déplacement :
dtvFFW
dtvOMd
OMdFMMFFW
RM
RM
)/(
)/(
)(Donc
')(
Puissance (instantanée) de
F
:
W;J
)(
)( )/(
PW
vF
dtFW
FP RM
B) Travail d’une force
A
B
M
OMd
M se déplace de A vers B, soumis à une force
F
dépendant éventuellement de la
position et du temps.
 BABA
M
BA OMdMFFW
B àA deallant
)()FW(")FW(")( 
Travail de
F
pour un déplacement de A à B
dtFPdtvFFW RM )()( )/(
Donc
  B
A
t
tBA
BA dtFPdtFPFW )()()(
C) Exemples
1) Forces perpendiculaires au déplacement
g
P
R
Travail élémentaire de
R
:
)/()/( car0)( RMRM vRdtvRRW 
Donc
0)RW()(
 BA BA RW 
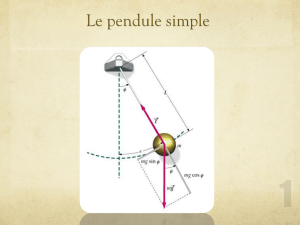
l
O fixe dans (R)
M(m)
P
T
e
e
Aspect énergétique de la mécanique du point

TeedlTOMdTTW  car0.)(
2) Force constante
On considère une force
F
indépendante de la position et du temps
(exemple : le poids à petite échelle)
ABFOMFOMdFOMdFFW B
A
BABA
BA    )(
3)
dtvdtvdtvFOMdFFW
vF
RMRM
RM
2
2
)/()/(
)/(
.)(
.
Supposons que M se déplace à module de vitesse constante :
LvttdtFW
v
L
vBA
tt
BAL
vv
AB
BA
BA
AB
RM
0
2
0
2
0
00
0)/(
.)(.v-.v-)(
B A deLongueur
Donc le travail de
F
dépend du chemin suivi et de la vitesse.
Remarque :
F
n’est constante que si M se déplace à vecteur vitesse
constant, et ainsi
)(
FW BA
vérifie aussi
ABFFW BA  
)(
4) Energie cinétique
a) Définition
Dans un référentiel (R), on considère un point matériel M de masse m,
de vitesse
)/(RM
v
. Alors
2
)/(
2)/( 2
1
.
2
1RMRMC vmvmE 
b) Théorème de l’énergie cinétique
On considère un référentiel (R) galiléen, un point matériel M de masse
m soumis à une résultante des forces
F
.
On a :
)/()/(
)/(
)/()/(
)/()/( ..
2
1RMRM
RM
RMRM
RMRC vam
dt
vd
vv
dt
vd
m
dt
dE 
(R) est galiléen.
Donc, d’après la relation fondamentale de la dynamique,
)/(
.RM amF 
Donc
 )/(
)/( RM RC vF
dt
dE 
)(
)/( FP
dt
dE RC 
Ou
OMdFdtvFdE RMRC  
.
)/()/(
soit
)(
)/( FWdE RC
Forme intégrale :
)()()( FWAEBE BACC
, ou
)()(
2
1
22 FWvvm BAAB
5) Application du théorème de l’énergie cinétique

a) Saut à ski
A
B
g
Un skieur part de A avec une vitesse nulle. Avec quelle vitesse décolle
t’il en B ? (On néglige les frottements)
ghv
zzhmghvm
PWPRWvmEE
B
BAB
BABABCC AB
2Donc
) (avec.
2
1
)()(.
2
1
2
2
b) Tir balistique
z
x
zflèche A
g
0
v
cos
0
vx 
indépendante du temps.
D’après le théorème de l’énergie cinétique appliqué à M entre O et A :
g
v
z
mgzvmvm
Oxvvv
mgzzzmgPWvmvm
O
AA
AAOOA
2
sin
Soit
.
2
1
cos.
2
1
Donc
//carcoset
)()(.
2
1
.
2
1
22
0
flèche
flèche
222
0
0
flèche0
22
II Energie potentielle
A) Force conservative
F
est dite conservative lorsque, pour tous points A et B de l’espace,
)(
FW BA
ne
dépend que de A et B et non pas de
BA
, soit
),()(
BAfFW BA 
Cas particulier :
A
Pour une boucle fermée,
0)(
FW AA
Exemple : le poids, une force constante.
Contre-exemple : frottement (pour une boucle,
ctev
, et sinon dépend du chemin)
B) Energie potentielle

On considère une force
F
conservative, et O fixe dans (R).
AB
O
F
est conservative.
Donc
),(),()()()()()( OBfOAfFWFWFWFWFW OBOABOOABA  
On définit la fonction
),()(: OMfMEME PP 
Ainsi,
)()(),(),()(
BEAEOBfOAfFW PPBA 
P
E
est l’énergie potentielle de M dans le champ de force
F
.
(On dit que
F
dérive de l’énergie potentielle
P
E
)
Soit
'
P
E
une autre fonction énergie potentielle. Soit A un point de l’espace.
Pour tout M de l’espace, on a :
)(')(')()()(
MEAEMEAEFW PPPPMA 
Donc
))()('()()('
M de teindépendan cte    AEAEMEME PPPP 
Donc
cte'  PP EE
Définition différentielle : Pour un déplacement infinitésimal de M à M’, on a :
)()'()(
')(
' MdEMEME
OMdFMMFFW
PPP
MM
Donc l’énergie potentielle est la fonction telle que
)()( MdEFW P
Méthode : On calcule
W
. Si on peut écrire
W
sous la forme
P
dEW
, alors
F
est conservative et
)cte(
P
E
est une énergie potentielle.
C) Exemples
1) Energie potentielle de pesanteur Epp.
dmgzmgdzkdzjdyidxkmgOMdPPW  )()( 
Donc
cte mgzEPP
2) Energie potentielle élastique
x
Ok,l0
M
e
e
On note
OMr
M se déplace dans le plan.
T
: tension du ressort
))(
2
1
()()()(
)()(
2
00
00
lrkddrlrkerdedrTOMdTTW
elrkellkT
Donc
cte
2
1
cte)(
2
122
0 kXlrkEPE
III Energie mécanique

A) Définition
M est soumis dans (R) galiléen à
i
F
forces conservatives d’énergies potentielles
pi
E
et
j
F
forces non conservatives.
On pose
iPiCm EEE
B) Théorème de l’énergie mécanique
D’après le théorème de l’énergie cinétique appliqué à M dans (R) galiléen, on a :
jj iPiC
jj iPiC
jj idE
iC
FWEEd
FWdEdE
FWFWdE
Pi
)()(
)(
)()(
jjm FWdE )( 
Ou
jj
mFP
dt
dE )( 
En intégrant la première relation, on obtient :
jjBAmmm FWAEBEE )()()(
Cas particulier : un système est dit conservatif lorsque
cte
m
E
C) Intégrale première du mouvement
L’intégrale première du mouvement, c’est l’équation différentielle du premier
ordre obtenue par application du théorème de l’énergie mécanique pour un système
conservatif.
1) Ressort horizontal
x
O M
Al0
i
k
ixOM
llOMx  0
Bilan des forces :
ikxillkT
kRR
kmggmP
z
)(
s)frottement de (pas
0
On a :
22 2
1
2
1kxmgzxmEm 