Les théorèmes de l`énergie

LES THEOREMES DE L’ENERGIE ET LES APPLICATIONS
I Théorème de l’énergie cinétique
Si on cherche à calculer les variations de l’énergie cinétique au cours du temps, on a vu que :
c
d dv
m v ma v
dt dt
Err r r
Si on se place dans un référentiel galiléen, on a :
ma F
r ur
, donc :
.
c
dF v F v
dt       
EP
ur r ur r
(0.1)
Théorème de l’énergie cinétique : Dans un référentiel galiléen, la dérivée par rapport au temps
de l’énergie cinétique d’un point matériel est égale à la somme des puissances des forces.
On peut écrire ce théorème sous forme différentielle :
c
d dt W     EP
(0.2)
Dans un référentiel galiléen, la différentielle de l’énergie cinétique correspond à la somme des
travaux élémentaires des forces
Ou sous forme de variation :
( ) ( )
c c f c i A B
t t W      E E E
(0.3)
Dans un référentiel galiléen, entre l’instant initial
i
t
où le point matériel est en
A
et le temps
f
t
où
le point matériel est en
B
, la variation de l’énergie cinétique correspond à la somme des travaux des
forces de
A
à
B
Exemple
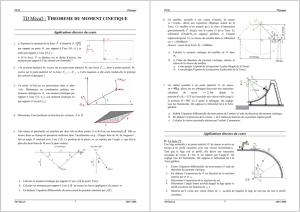
(1) On étudie un point matériel M(m) dans un référentiel du laboratoire
supposé galiléen.
(2) Les puissance (ou travaux ) en jeu sont :
( ) . sin
( ) . 0
P mg mg v mg
P T T v
(3) Théorème de l’énergie cinétique
1
( ² ²)
2² sin
dm
dEc P m mg
dt dt
d’où
sin 0
g
Remarque : on peut aussi
0
( ) ( cos ) ( ² ² ²)
2
m
W mg xf xi mg Ec v
que l’on dérive pour obtenir
sin 0
g

II Théorème de l’énergie mécanique
Soit un point matériel
M
soumis à des forces conservatives
C
F
ur
qui dérivent d’une énergie
potentielle
p
E
,et des forces non conservatives
NC
F
ur
qui ne dérivent pas d’une énergie potentielle.
Le travail élémentaire des forces s’écrit :
C NC p NC
W W W d W     E
Le théorème de l’énergie cinétique donne :
c p NC
d W d W    EE
Soit :
m c p c p NC
d d d d W     E E E E E
(0.4)
Dans un référentiel galiléen, la différentielle de l’énergie mécanique correspond au travail
élémentaire des forces non conservatives.
Ou :
mNC
ddt  EP
(0.5)
Dans un référentiel galiléen, la dérivée par rapport au temps de l’énergie mécanique d’un point
matériel est égale à la somme des puissances des forces non conservatives.
Ou encore :
( ) ( ) NC
m m f m i A B
t t W     E E E
(0.6)
Dans un référentiel galiléen, entre l’instant initial
i
t
où le point matériel est en
A
et le temps
f
t
où
le point matériel est en
B
, la variation de l’énergie mécanique correspond au travail des forces non
conservatives de
A
à
B
.
Propriétés :
 Intégrale première de l’énergie : Si le point matériel n’est soumis qu’à des forces
conservatives, ou que le travail des forces non conservatives est nul alors dans ce cas,
l’énergie mécanique est constante au cours du mouvement.
 En présence de forces non conservatives, en général
0
NC
AB
W
donc
( ) ( )
m f m i
ttE E
Que devient l’énergie disparue ? énergie interne et chaleur
 Contrairement aux travaux les énergies sont des fonctions d’état.
Exemple
On étudie le solide ramené à son barycentre dans le référentiel lié
au solide supposé galiléen. Le contact solide-solide se fait avec un
frottement de coefficient, on cherche la vitesse initiale nécessaire
pour arriver en haut.
Bilan des travaux en jeu :
( ) cos
sin
T T T N
h
W R R avec R fR fmg
(en projetant
le PFD sur l’axe la normale).
Théorème de l’énergie mécanique :
0
1
0 ² 0
2
Emf Emi Ecf Epf Eci Epi mgh mv        
02 (1 cot )v gh f an

III Etude des états d’équilibre d’un système à un degré de liberté
V1 Position du problème
De nombreuses études en physique où l’énergie mécanique est constante ,se ramènent à l’étude
d’un problème à un degrés de liberté (r,x,,T..) dont on connaît l’énergie potentielle Ep(x)
(mouvement des planètes, molécule diatomique , ionisation , solide en rotation autour d’un axe ..).
Quand cette énergie potentielle est une fonction complexe, l’équation différentielle du
mouvement obtenue avec le théorème de l’énergie est très peu souvent soluble. On peut pourtant
procéder à une étude qualitative du mouvement et des ses états intéressants : les états
d’équilibres.
On part du principe
0Em cte Ec Ep Ep car Ec    
connaissant Ep
Exemple : ici énergie potentielle d’une comète qui subit l’attraction solaire ou énergie
d’interaction entre deux atomes d’une molécule diatomique.
(1)
1
0Em x x  
on parle d’état libre (comète qui
s’échappe de l’influence du soleil ou molécule séparée)
(2)
0 2 3
,0 ,Em E x x x  
on parle d’état lié(comète
qui tourne autour du soleil ou molécule excitée)
(3)
00
Em E x x  
on parle d’état lié d’équilibre
stable (comète qui tourne autour du soleil sur une
trajectoire circulaire ou molécule au repos)
Propriété :
Les minima de l’énergie potentielle
²
00
²
dEp d Ep
et
dx dx
correspondent aux états d’équilibre
stable d’un système et les maxima aux états instables.
Démonstration :
Si
0
x
est un minimum de Ep alors :
00
0 0 0 0 0
( )² ( )²
²
( ) ( ) ( ) ( ) ( ) ( )
2 ² 2
x x x x
dEp d Ep
Ep x Ep x x x x x Ep x K
dx dx
avec K > 0.
Rappel :une fonction f(x) définie continue dérivable autour de x0 admet en x0 un minimum (resp
maximum) ssi
0 0 0
²²
( ) 0 ( ) 0 ( ) 0
²²
df d f d f
x et x resp x
dx dx dx
Alors
0
00
0
() ()
0
pxx
si x x
dx
F e K x x e si x x
dx
E
ur r r
équivalente à une force de rappel (car K >
0) qui « ramène » x vers x0 d’où l’équilibre stable.
D’autre part le PFD « proche » de x0 devient alors
0 0 0
( ) ( ) cos( )
m
KK
mx K x x x x x x t x X t
mm
où  est la pulsation des
petites oscillations autour de l’équilibre.
A contrario , Si
0
x
est un maximum de Ep alors l’équilibre est instable.

VI-2 Exemple : le pendule simple
a) Position du problème
On étudie un point matériel M(m) dans un référentiel du laboratoire supposé
galiléen de vitesse initiale v0.
Calcul de l’énergie potentielle fonction de  :
. cos (1 cos )dEp Pdr mgdx Ep mgx cte mgl cte mgl
si
Ep(0)=0
La puissance des forces non conservative est nulle.
Théorème de l’énergie mécanique
1² ² (1 cos )
2
Em Ec Ep cte ml mgl
et
0 sin
dEm mgl ml
dt
d’où
sin 0
g
équation différentielle insoluble.
b) Etude qualitative
C’est un problème à un degré de liberté  à énergie mécanique constante . Traçons Ep().
2
0
0.5Em mv
(1)
2Em mgl
Tous les angles sont atteints (état libre)
(2)
0,2Em mgl
oscillation (non sinusoïdale) entre 1 et 2.
(3)
00Em
on parle d’état lié d’équilibre stable.
(4) Impossible.
 Etats d’équilibre : extréma de Ep
0 0,
dEp
d
 Stabilité de ces états :
0 0 '
²cos 0'
²
si état d équilibre stable
d Ep mgl si état d équilibre instable
d
 Période des petites oscillations autour des positions d’équilibre :
00
²
( ) ( ) 0 0
2²
si e
e d Ep
Ep Ep e si e
d
d’où
1
( ) ² ² ( )
22
e
Em cte ml Ep e K
d’où
( ) cos 0
K K K
e t e A t si K
ml ml ml
Ici l’état d’équilibre stable est 0 :
( ) cos g t A t
l
En = la solution est exponentielle.