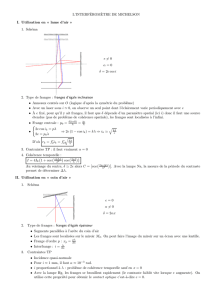
I- Interféromètre de Michelson et planéité d`un miroir

◦
δϕ =
2π
λ2e0+π
π
ε(M)=2ε01−cos(4πe0
λ)
ε(e0)λ/2
e0
ε
e0= 0 ε(e0)
e0=pλ
2p∈Z
e0= 0
e0
e0
x
δϕ =2π
λ2e(M) + π=2π λ2αx +π
p=δ
λ=2αx λ+1 2p x(p) = λ 2α(p−1)
i=λ
2|α|
δθ =π
60×180 = 3.10−4
imin
imin =P P ×θmin ≈10−4αλ
2|α|> imin ⇒ |α|<λ 2imin <3.10−3
e(P) = e0+R−√R2−r2=e0+R−R1−r2
R21/2e≈e0+r2 2RrR
2e(P)
π δϕ(P) = 2π
λ2e(P) + π⇒δϕ(P) = π4e0+r2
2R
λ+ 1
P C P C∗
1P C∗ 2◦

2
r
OA =−2f0
1
2f0+1
OA0=1
f0⇒1
OA0=1
f0−1 2f0=1 2f0OA0= 2f02f0
−1
γ=A0B0
AB =−10 =
−f0
AF ⇒AF =−f0
γ⇒AO =AF +F O =−f0 γ+f0=γ−1 γf0
11
10 f0
p0=δ(r=0)
λ⇒p0=2e0 λ+1 2
R1p1k Rk
pk=p1+k−1r k −1 = R2
k−R2 1
λR ⇒
Rk=pR2
1+ (k−1)λR
r(p)
p
2e0
λ+r2(p) λR +1 2=p⇒r(p) = sλR p−1 2−2e0 λ
r(p)e0e0
e0
p1+k−1 = 2e0
λ+R2
k
λR +1 2
p1+k=2e0
λ+R2
k+1
λR +1 2R=R2
k+1−R2 k
λ
tan iA=xA
f0xA= 0 A0F0
A A0
T1T2δ0= 0
δ0= 0
δ|δ|< lclc
F0
T1T2
IA=I1+I2+ 2√I1I2cos 2π
λδ= 2I11 + cos 2π λδ δ
δ=a(im)⇒δ=a x
f0
IA= 2I1h1 + cos 2π
λ
a
f0xi i=λf0 a
F0y i F 0
P C P C∗
1P C∗ 2◦

tan iB=xB
f0xB=f0iB
IB=I1+I2+ 2√I1I2cos 2π
λδ= 2I11 + cos 2π λδ δ
δ=a(im−iB)⇒δ=a
f0(x−xB)
IB= 2I1h1 + cos 2π
λ
a
f0(x−xB)i
i=λf0
a
IASB(x) = IA+IB= 2I12 + cos 2π
λ
a
f0x+ cos 2π λ
a
f0(x−xB)
IASB(x)=4I1h1 + cos π
λ
a
f0(2x−xB)cos π λ
a
f0xBi
cos π
λ
a
f0xB= 0 π λ
a
f0xB=π 2+kπ k ∈Z a =
λf0
xB1 2+k⇒a=λ iB1 2+ka7→ 0
iB=λ
2a
imin amax imin =λ
2amax =2×10−6 2×100 = 1,0×10−8rad = 21msec
˜
A0
ω=2π c
λrad ·s−1
~
k0=2π
λ~uzrad ·m−1
P C P C∗
1P C∗ 2◦

t(x, y) = cos2πx
acos2πy a= 0 ⇔cos πx a= 0 cos πy a= 0
x=(1 + 2 p)a
2p∈Z y =(1 + 2 q)a 2q∈Z
a x y
t(x, y) = cos2πx
acos2πy a=ejπx
a+e−jπx a
22ejπy
a+e−jπy a
22
t(x, y) = 1
16 hej2πx
a+2+e−j2πx aej2πy a+2+e−j2πy ai
t(x, y) = 1
16 h2ej2πx
a+ 4 + 2e−j2πx a+ej2π(y+x) a+ 2ej2πy a+ej2π(y−x) a+ej2π(−y+x) a+ 2e−j2πy a+e−j2π(y+x) ai
˜
A(~r, t) =
N
X
n=1
˜
Ane−j(ω t−~
kn·~r)
knx
2π
a−2π a
2π
a−2π a
2π
a−2π a
kny
2π
a
2π
a
2π
a−2π a−2π a−2π a
An2˜
A0
16 4˜
A0
16 2˜
A0
16
˜
A0
16 2˜
A0
16
˜
A0
16
˜
A0
16 2˜
A0
16
˜
A0
16
kn=ω
c=2π λ
aλ|knx|  kn|kny|  knknz≈kn=2π
λ
f0λ σ =f0λ
a
•0,0 16 I0
•f0λ
a,0 4 I0
P C P C∗
1P C∗ 2◦

• −f0λ
a,0 4 I0
•0,f0λ
a4I0
•0,−f0λ
a4I0
• −f0λ
a,−f0λ aI0
• −f0λ
a,+f0λ aI0
•+f0λ
a,−f0λ aI0
•+f0λ
a,+f0λ aI0
2f0
~
kn~uy
2f0λ
a
˜
A(~r, t) =
N
P
n=1
˜
Ane−j(ω t−~
kn·~r)
knx
2π
a−2π a
kny
knz
2π
λ
2π
λ
2π
λ
An2˜
A0
16 4˜
A0
16 2˜
A0
16
P C P C∗
1P C∗ 2◦