trigonometrie

3ème – Chapitre 10 Trigonométrie
© S.DUCHET – http://epsilon.2000.free.fr 1 / 2
T
TR RI IG GO ON NO OM ME ET TR RI IE E
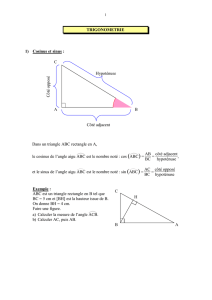
définitions
Si ABC est un triangle rectangle en C, on définit :
 le cosinus de l'angle A, noté
cos( )A, le quotient :
cos( ) AC coté adjacent à A AAB hypoténuse  ;
 le sinus de l'angle
A
, noté sin( )
A
,
le quotient :
sin( )
B
C coté opposé à A
AAB hypoténuse  ;
 la tangente de l'angle
A
, noté
tan( )A, le quotient :
tan( )
B
C coté opposé à A
AAC coté adjacent à A  ;
exemple
ABC est un triangle rectangle en B tel que
5
A
Bcm et
() 33mes A .
Calculer ()mes C , BC et AC (on arrondira les
longueurs au dixième).
90 33 57 donc
() 57mes C .
cos( ) AB AAC  (car [AB] est le côté adjacent à l'angle A).
5
cos(33)
A
C
cos(33) 5AC
56
cos(33)
AC . [AC] mesure environ 6 cm.
tan( )
B
C
A
A
B
 (car [BC] est le côté opposé à l'angle
A
et [AB] est le côté adjacent à l'angle
A
).
tan(33) 5
B
C
5tan(33) 3,2BC   . [BC] mesure environ 3,2 cm.
B
C
A
hypoténuse
côté opposé à l'angle
A
côté adjacent à l'angle
A
C
A
B

3ème – Chapitre 10 Trigonométrie
© S.DUCHET – http://epsilon.2000.free.fr 2 / 2
Autre exemple :
ABC est un triangle rectangle en C tel que 7
A
Bcm et 4
B
Ccm . Calculer la mesure des angles
B
AC
et
ABC .
Dans le triangle ABC rectangle en C :
sin( )
B
C
BAC AB
4
sin( ) 7 BAC 
1
()sin(4:7)35mes BAC 
1
cos( )
4
cos( ) 7
()cos(4:7)55
BC
ABC AB
ABC
mes ABC 
propriétés
Si x désigne la mesure d'un angle aigu, on a les relations suivantes :
22
cos sin 1xx
sin
tan cos
x
x
x
.
Preuve
On se place dans un triangle ABC rectangle en B. Appelons x la mesure en degrés de l'angle
B
CA :
sin AB xAC , cos
B
C
xAC  et tan AB
x
B
C
.
22
22
22
2
2
2
(sin ) (cos )
1
AB BC
xx
AC AC
AB BC
AC
AC
AC
sin tan
cosxABACAB
x
xACBCBC
 .
A
B C
C
A
B
car 22 2
AB BC ACd'après
le théorème de Pythagore