Fonction exponentielle

TaleST I Fonction exponentielle 2008/2009
Fonction exponentielle
Table des matières
I Introduction de l’exponentielle 2
I.1 Définition ............................................... 2
I.2 Relation fondamentale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
II Etude de la fonction exponentielle 3
II.1 Limite aux bornes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
II.2 Variations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
II.3 Fonction exp(u)............................................ 4
II.4 Croissance comparée de l’exponentielle et des fonctions puissance . . . . . . . . . . . . . . . . 5
III Résolution d’équations 5
IV Exerçice de bac 6
Bref histoirique : Le professeur Carl B. Boyer, indique qu’Archimède a exprimé de grands nombres en
utilisant une formulation qui s’apparente à une exponentielle dans son traité sur les grains de sables (Psam-
mites). Apollonius de Perga s’est aussi approché des exponentielles, en s’intéressant aux grands nombres
avec l’usage de ses "tetrades".
Au Moyen Age, Thomas Brawardine, a fait un pas en direction de l’étude des fonctions transcendantales.
Nicole Oresme l’a suivi en généralisant sa théorie des proportions. Il a aussi étudié, entre autres choses, la
fonction x à la puissance racine de deux.
http://nathalie.daval.free.fr -1-

TaleST I Fonction exponentielle 2008/2009
I Introduction de l’exponentielle
I.1 Définition
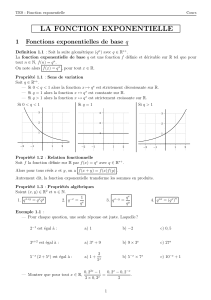
Définition 1
La fonction exponentielle, est la fonction définie sur Rpar exp(x) = ex,exétant l’unique nombre réel
positif dont le logarithme vaut x
Remarque 1
On dit que la fonction exponentielle est la fonction réciproque de la fonction logarithme, ce qui signifie que
graphiquement, les courbes sont symétriques par rapport à la première bissectice (y=x).
Conséquences directes :
•exp(x)>0.
•exp(1) = e1=e≈2,718.
•ln(ex) = x.
•eln(x)=x.
•Pour tout x∈Ret tout y > 0 : y=ex⇐⇒ ln(y) = x.
Propriété 1
Soit uune fonction continue et définie sur I, alors la fonction x7→ exp[u(x)] est définie et existe sur I.
Exemple 1
Ensemble de définition Dfde la fonction définie par f(x) = ex+3 :
➔La focntion x7→ x+ 3 est définie, continue sur R.
➔D’où : Df=R.
I.2 Relation fondamentale
Propriété 2
Pour tous réels aet b, on a la relation fondamentale suivante :
exp(a+b) = exp(a)×exp(b) ou encore ea+b=ea×eb.
Démonstration :
Soient x, y ∈R. On a ln(ex+y) = x+y= ln(ex) + ln(ey) = ln(ex×ey).
En appliquant l’exponentielle de chaque côté, il vient :
eln(ex+y)=eln(ex×ey)⇐⇒ ex+y=ex×ey.
http://nathalie.daval.free.fr -2-

TaleST I Fonction exponentielle 2008/2009
Propriété 3
Soient aet bdeux réels et nest un entier relatif, alors :
♦1
ea=e−a.
♦ea
eb=ea−b.
♦(ea)n=ean.
En résumé, l’exponentielle a la particularité de transformer les sommes en produits, les différences en quo-
tients et les multiplications en puissances. (inversement au logarithme !).
Remarque 2
La propiété fondamentale se généralise au cas d’un produit de trois, quatre, nfacteurs :
exp(a1+a2+...+an) = exp(a1)×exp(a2)× · · · × exp(an).
Exemple 2
Transformations d’expressions numériques :
➔e2×e3=e6.
➔1
e5=e−5.
➔e7
e2=e5.
➔(e−2)−3=e6.
Exemple 3
Transformations d’expressions algébriques :
➔ex+3 ×e2x+1 =e(x+3)+(2x+1) =e3x+4.
➔e3x−2×e−4x+2
ex2=e(3x−2)+(−4x+2)−(x2)=e−x−x2.
➔(ex−2)2=e2x−4.
II Etude de la fonction exponentielle
II.1 Limite aux bornes
Propriété 4
On a les limites importantes suivantes :
lim
x→−∞ ex= 0 lim
x→+∞ex= +∞.
Conséquence : La droite y= 0 est donc asymptote orizontale à la courbe représentative de la fonction
exp.
http://nathalie.daval.free.fr -3-

TaleST I Fonction exponentielle 2008/2009
Exemple 4
Limite en +∞de ex−1:
➔lim
x→+∞(x−1) = +∞
lim
X→+∞
eX= +∞)par composition : lim
x→+∞ex−1= +∞.
Limite en −∞ de ex+3 :
➔lim
x→−∞(x+ 3) = −∞
lim
X→−∞
eX= 0 )par composition : lim
x→−∞
ex+3 = 0.
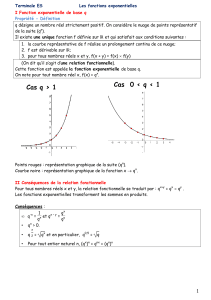
II.2 Variations
Propriété 5
La fonction exponentielle est dérivable sur Rde dérivée (ex)′=ex.
Démonstration :
Ce point est une conséquence de la dérivation des fonctions composées :
On dérive la relation ln ex=x:(ex)′
ex= 1 d’où (ex)′=ex.
Sachant que la dérivée de la fonction exponentielle est exet qu’elle est définie sur R, la dérivée est strctement
positive, et la fonction est donc strictement croissante sur cet intervalle.
D’où le tableau de variations et la courbe :
x−∞ 0 +∞
f′(x) +
+∞
fր
0
signe +
1
2
3
4
−1
1 2 3 4−1−2−3−4−5
y= exp(x)
e≈2,718
II.3 Fonction exp(u)
Propriété 6
Soit uune fonction définie dérivable sur I, alors la fonction x→exp[u(x)] est dérivable sur Ide dérivée
exp[u(x)]′=u′(x) exp[u(x)].
On écrit aussi : (eu)′=u′eu.
http://nathalie.daval.free.fr -4-

TaleST I Fonction exponentielle 2008/2009
Exemple 5
Soit fla fonction définie par f(x) = ex2+1.
➔Le polynôme udéfini par u(x) = x2+ 1 est défini et dérivable sur Rde dérivée u′(x) = 2x.
➔Donc, fest dérivable sur Ret f′(x) = 2x ex2+1.
Soit gla fonction définie sur Rpar g(x) = ex−2.
➔Le polynôme vdéfini par v(x) = x−2est défini et dérivable sur Rde dérivée v′(x) = 1.
➔Donc, gest dérivable sur Ret g′(x) = g(x) = ex−2.
II.4 Croissance comparée de l’exponentielle et des fonctions puissance
Propriété 7
On a les limites classiques suivantes, pour tout n∈N∗:
♦lim
x→+∞
ex
x= +∞.
♦lim
x→+∞
ex
xn= +∞.
♦lim
x→−∞ x ex= 0.
♦lim
x→−∞ xnex= 0.
Remarque 3
On dit que "l’exponentielle l’emporte sur la puissance".
L’idée à retenir : Au voisinage de +∞, les fonctions x→ln x,x→xαet x→exprennent des valeurs qui
se classent dans cet ordre de la plus petite à la plus grande.
III Résolution d’équations
Propriété 8
Pour tout uet v, on a les résultats suivants :
♦L’équation exp(u) = exp(v) possède comme unique solution u=v.
♦Pour tout λ > 0, l’équation exp(u) = λpossède comme unique solution le nombre u= ln(λ).
Exemple 6
Résolution dans Rde l’équation ex= 4 :
➔ex= 4 ⇐⇒ ln(ex)) = ln(4) ⇐⇒ x= ln 4.
Résolution dans Rde l’équation 2ex×e(3x) = 5 :
➔2ex×e3x= 5 ⇐⇒ 2ex+3x= 5 ⇐⇒ e4x=5
2⇐⇒ 4x= ln 5 2⇐⇒ x=1 4ln 5 2.
Résolution dans Rde l’équation exp(−x2+ 9) = 1.
➔exp(−x2+ 9) = 1 ⇐⇒ ln[exp(−x2+ 9)] = ln(1) ⇐⇒ −x2+ 9 = 0 ⇐⇒ x2= 9 ⇐⇒ x=−3, ou x= 3.
http://nathalie.daval.free.fr -5-