RAPPELS ET COMPLÉMENTS SUR LES FONCTIONS

Christophe Bertault — Mathématiques en MPSI
RAPPELS ET COMPLÉMENTS SUR LES FONCTIONS
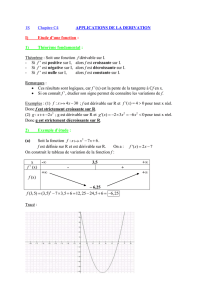
1VOCABULAIRE USUEL SUR LES FONCTIONS
1.1 VALEURS D’UNE FONCTION
Définition (Ensemble de définition et image d’une fonction, image et antécédents d’un point) Soient Aune partie
de Ret f:A−→ Rune fonction.
•L’ensemble Aest appelé l’ensemble de définition de f et tout réel f(x)avec x∈Aest appelé une valeur de f .
•Pour tous x∈Aet y∈R, si y=f(x), on dit que yest L’image de x par f et que xest UN antécédent de y par f .
y=f(x)
y
x1x2x3
Explication Sur la figure ci-contre, ypossède plusieurs antécédents par f,
raison pour laquelle on parle d’UN antécédent et non de « l’ » antécédent de y.
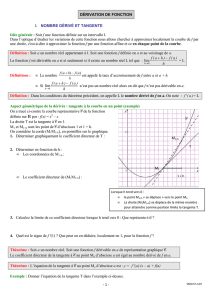
Définition (Image d’une partie par une fonction, image d’une fonction) Soient Aune partie de Ret f:A−→ Rune
fonction.
•Pour toute partie A′de A, on appelle image de A′par f , notée f(A′), l’ensemble :
f(A′) = ¦y∈R/∃x∈A′/y=f(x)©=¦f(x)©x∈A′.
•L’image de Atout entier est simplement appelée l’image de f et notée généralement Im fplutôt que f(A).
տ ր
A′
ր
ց
f(A′)
Explication L’image f(A′)de A′par fest l’ensemble des images par fdes
éléments de A′. Graphiquement, pour déterminer f(A′), on projette sur l’axe des ordonnées
la portion du graphe de fqui se situe au-dessus de A′, comme l’illustre la figure de droite.
Im fOn fait pareil pour déterminer graphiquement l’image
Im fde f, mais avec le graphe de ftout entier.
Exemple
•L’image de R+par la fonction exponentielle est l’intervalle [1,+∞[. L’image de R−est ]0,1].
•L’image de πZpar la fonction sinus est 0, l’image de [0,π]est [0,1], l’image de h−π
2,π 2iest [−1,1]et l’image de
[0,2π]est aussi [−1, 1].
Définition (Expression « à valeurs dans. . . ») Soient Aet Bdeux parties de Ret f:A−→ Rune fonction. On dit que
fest à valeurs dans B si toute valeur de fest élément de B, i.e. si : ∀x∈A,f(x)∈B, ou encore si : Im f⊂B.
$ATTENTION !$Dire que fest à valeurs dans B, ce n’est pas dire que l’image de fest Btout entier. La fonction
x7−→ |x|+1, par exemple, est définie sur Ret à valeurs dans R+, mais son image n’est pas R+tout entier mais seulement
[1,+∞[— car quand xdécrit R+,|x|+1 décrit [1,+∞[.
1

Christophe Bertault — Mathématiques en MPSI
1.2 COMPOSITION DES FONCTIONS
Définition (Composée de deux fonctions) Soient Aet Bdeux parties de Ret f:A−→ Ret g:B−→ Rdeux fonctions.
On suppose fà valeurs dans B. On appelle composée de f suivie de g la fonction g◦fdéfinie sur Apar :
∀x∈A,g◦f(x) = gf(x).
Explication Pourquoi la condition « fest à valeurs dans B» est-elle si importante ? Pour pouvoir parler de gf(x)
pour tout x∈A, on doit garantir que f(x)appartient à l’ensemble de définition Bde gpour tout x∈A:∀x∈A,f(x)∈B,
autrement dit que fest à valeurs dans B.
Exemple La fonction x7−→ ln(2x+3)est définie sur −3
2,+∞.
En effet La fonction x7−→ 2x+3 est définie sur Ret la fonction ln sur R∗
+, mais quand xdécrit R, 2x+3
n’appartient pas forcément à R∗
+. Pour quels x∈Rest-il vrai que : 2x+3>0 ? Réponse : x∈−3
2,+∞.
x−∞ −1 1 +∞
1+x−0+
1−x+0−
1−x2−0+0−
Exemple La fonction x7−→ p1−x2est définie sur [−1,1].
En effet La fonction x7−→ 1−x2est définie sur Ret la fonction p·
sur R+, mais quand xdécrit R, 1 −x2n’appartient pas forcément à
R+. Pour quels x∈Rest-il vrai que : 1−x2= (1+x)(1−x)¾0 ?
Réponse : x∈[−1, 1].
$ATTENTION !$La composition n’est pas commutative, ne confondez pas g◦fet f◦g. Il arrive d’ailleurs souvent
que l’une de ces fonctions soit définie sans que l’autre le soit. Par exemple, si fest la fonction x7−→ x2et si gla fonction
x7−→ x2+1, toutes deux définies sur R,g◦fest la fonction : x7−→ x22+1=x4+1 et f◦gla fonction :
x7−→ x2+12=x4+2x2+1. Ce n’est pas pareil !
Théorème (Associativité de la composition) Soient A,Bet Ctrois parties de Ret f:A−→ R,g:B−→ Ret
h:C−→ Rtrois fonctions. On suppose fà valeurs dans Bet gà valeurs dans C. Alors :
h◦(g◦f) = (h◦g)◦f.
Exemple La fonction x7−→ 1+epx
xp2−xest définie sur ]0, 2[.
En effet La construction de cette fonction requiert plus qu’une simple composition, également des sommes,
produits et quotients.
◦
◦
×
+
÷
x7−→ 2−x
x7−→ px
x7−→ px
x7−→ ex
x7−→ p2−x
x7−→ x
x7−→ epx
x7−→ 1
x7−→ xp2−x
x7−→ 1+epx
x7−→ 1+epx
xp2−x
La quantité 1+epx
xp2−xest bien définie
si et seulement si : xp2−x6=0, px∈R, 2 −x¾0 et x¾0,
i.e. si et seulement si : x6=0, x6=2, x¶2 et x¾0, i.e. x∈]0,2[.
2

Christophe Bertault — Mathématiques en MPSI
1.3 FONCTIONS MONOTONES,FONCTIONS MAJORÉES/MINORÉES
Définition (Monotonie) Soient Aune partie de Ret f:A−→ Rune fonction.
•On dit que fest croissante si : ∀x,y∈A,x<y=⇒f(x)¶f(y).
•On dit que fest strictement croissante si : ∀x,y∈A,x<y=⇒f(x)<f(y).
•On dit que fest décroissante si : ∀x,y∈A,x<y=⇒f(x)¾f(y).
•On dit que fest strictement décroissante si : ∀x,y∈A,x<y=⇒f(x)>f(y).
•On dit que fest (resp. strictement)monotone si fest (resp. strictement) croissante ou décroissante.
Explication On peut bien sûr CARACTÉRISER la monotonie d’une fonction DÉRIVABLE par le signe de sa dérivée,
mais c’est là un THÉORÈME et non une DÉFINITION. La définition ci-dessus est générale et ne requiert pas la dérivabilité.
Théorème (Somme de fonctions monotones) Soient Aune partie de Ret f:A−→ Ret g:A−→ Rdeux fonctions.
Si fet gsont croissantes, alors f+gl’est aussi. Si de plus fou gl’est strictement, alors f+gaussi.
On dispose d’un résultat analogue pour les fonctions décroissantes.
Démonstration Dans le cas où fest croissante et gstrictement croissante, soient x,y∈Aavec x<y.
Comme fest croissante : f(x)¶f(y), et comme gest strictement croissante : g(x)<g(y), donc
par somme : f(x) + g(x)<f(y) + g(y).
Exemple Pas besoin de dériver pour expliquer que la fonction x7−→ x+ln xest strictement croissante sur R∗
+!
Théorème (Composée de fonctions monotones) Soient Aet Bdeux parties de Ret f:A−→ Ret g:B−→ Rdeux
fonctions. On suppose fà valeurs dans B.
•Si fet gsont (resp. strictement) monotones de même sens de variation, alors g◦fest (resp. strictement) croissante.
•Si fet gsont (resp. strictement) monotones de sens de variation opposés, alors g◦fest (resp. strictement)
décroissante.
Démonstration Dans le cas où fest croissante et gdécroissante, soient x,y∈Aavec x<y. Comme fest
croissante : f(x)¶f(y), puis comme gest décroissante : gf(y)¶gf(x).
Exemple Pas besoin de dériver pour expliquer que la fonction x7−→ eexest strictement croissante sur R!
Définition (Fonction majorée/minorée/bornée) Soient Aune partie de Ret f:A−→ Rune fonction.
•On dit que fest majorée sur A si : ∃M∈R/∀x∈A,f(x)¶M. Un tel réel Mest appelé UN majorant de
f sur A. On dit ausi que fest majorée par M sur A ou que M majore f sur A.
•On dit que fest minorée sur A si : ∃m∈R/∀x∈A,f(x)¾m. Un tel réel mest appelé UN minorant de f
sur A. On dit aussi que fest minorée par m sur A ou que m minore f sur A.
•On dit que fest bornée sur A si fest à la fois majorée et minorée sur A, i.e. si : ∃K∈R+/∀x∈A,
f(x) ¶K.
Fonction majorée non minorée Fonction minorée non majorée Fonction bornée
3

Christophe Bertault — Mathématiques en MPSI
Démonstration Par définition, la proposition « fest majorée et minorée sur A» s’écrit :
∃m,M∈R/∀x∈A,m¶f(x)¶M,
or ce n’est pas la définition donnée ci-dessus. Montrons donc l’équivalence des deux formulations.
•Si : ∃K∈R+/∀x∈A,
f(x) ¶K, alors : −K¶f(x)¶K, donc fest minorée et majorée.
•À présent, si : ∃m,M∈R/∀x∈A,m¶f(x)¶M, posons : K=max ¦|m|,|M|©. Alors
pour tout x∈A:−K¶−|m|¶m¶f(x)¶M¶|M|¶K, donc : 
f(x) ¶K.
Définition (Maximum/minimum d’une fonction) Soient Aune partie de R,f:A−→ Rune fonction et a∈A.
•On dit que f admet un maximum en a si pour tout x∈A:f(x)¶f(a). Le réel f(a)est alors appelé le
maximum de fen a, on le note aussi max
Afou max x∈Af(x).
•On dit que f admet un minimum en a si pour tout x∈A:f(x)¾f(a). Le réel f(a)est alors appelé le
minimum de fen a, on le note aussi min
Afou min x∈Af(x).
Maximum atteint deux fois
Pas un minimum
mais un minimum local
(notion étudiée plus tard)
Pas un maximum
mais un maximum local
(notion étudiée plus tard)
Pas de minimum
$ATTENTION !$Une fonction peut ne pas avoir de maxi-
mum/minimum et quand elle en a un, il peut être atteint en plusieurs
points différents.
1.4 TRANSFORMATIONS AFFINES DU GRAPHE D’UNE FONCTION
Théorème (Transformations affines du graphe d’une fonction, cas des symétries) Soient Aune partie de Ret
f:A−→ Rune fonction. Les graphes ci-dessous sont représentés dans un repère orthonormal O,−→ ı,−→ .
O
−→
ı
−→
y
=
f
(
x
)
y
=
−
f
(
x
)
O−→
ı
−→
y
=
f
(
x
)
y
=
f
(
−
x
)
•La fonction x7−→ −f(x)est définie sur Aet
son graphe s’obtient à partir de celui de f
par une symétrie par rapport à (Ox).
•La fonction x7−→ f(−x)est définie sur −A,
i.e. le symétrique de Apar rapport à (O y),
et son graphe s’obtient aussi à partir de celui
de fpar la même symétrie.
Théorème (Transformations affines du graphe d’une fonction, cas des translations) Soient Aune partie de Ret
f:A−→ Rune fonction. Les graphes ci-dessous sont représentés dans un repère orthonormal O,−→ ı,−→ .
O−→
ı
−→
y
=
f
(
x
)
y
=
f
(
x
)
+
y
0
y0−→
O−→
ı
−→
y
=
f
(
x
)
y
=
f
(
x
+
x
0
)
−x0−→
ı•Soit y0∈R. La fonction x7−→ f(x) + y0est défi-
nie sur Aet son graphe s’obtient à partir de celui
de fpar une translation de vecteur y0−→
.
•Soit x0∈R. La fonction x7−→ f(x+x0)est dé-
finie sur A−x0, i.e. l’ensemble Adécalé vers la
gauche de x0, et son graphe s’obtient à partir de
celui de fpar une translation de vecteur −x0−→
ı.
$ATTENTION !$Dans le cas de la fonction x7−→ f(x+x0), il y a bien un signe « moins » dans l’expression du vecteur
de translation −x0−→
ıet c’est normal, la fonction x7−→ f(x+x0)atteint la valeur f(0)en −x0, puis la valeur f(1)en −x0+1,
etc. Pour résumer, on peut dire que x7−→ f(x+x0)est EN AVANCE de x0sur x7−→ f(x).
4

Christophe Bertault — Mathématiques en MPSI
Théorème (Transformations affines du graphe d’une fonction, cas des contractions/dilatations) Soient Aune
partie de Ret f:A−→ Rune fonction. Les graphes ci-dessous sont représentés dans un repère orthonormal O,−→ ı,−→ .
O−→
ı
−→
y
=
f
(
x
)
y
=
λ
f
(
x
)
Dilatation verticale (λ¾1)
O−→
ı
−→
y
=
f
(
x
)
y
=
λ
f
(
x
)
Contraction verticale (λ < 1)
•Soit λ > 0. La fonction x7−→ λf(x)est dé-
finie sur Aet son graphe s’obtient à partir
de celui de fpar une dilatation verticale de
rapport λsi λ¾1 et une contraction verti-
cale de rapport 1
λsi λ < 1.
O−→
ı
−→
y=f(x)
y=f(λx)
Contraction horizontale (λ¾1)
O−→
ı
−→
y=f(x)
y=f(λx)
Dilatation horizontale (λ < 1)
•Soit λ > 0. La fonction x7−→ f(λx)est définie
sur l’ensemble dilaté/contracté 1
λAet son graphe
s’obtient à partir de celui de fpar une contrac-
tion horizontale de rapport λsi λ¾1 et une di-
latation horizontale de rapport 1
λsi λ < 1.
Exemple
y=sin xy=sin(x+1)y=sin(2x+1)
y=sin(2x+1)
2y=−sin(2x+1) 2y=1−sin(2x+1)
2
Définition (Parité/imparité)
Soit Aune partie de Rsymétrique par rapport à 0, i.e. telle que :
∀x∈A,−x∈A.
Soit f:A−→ Rune fonction.
•On dit que fest paire si : ∀x∈A,f(−x) = f(x).
Cela revient à dire que le graphe de fest symétrique par rapport à l’axe des or-
données.
•On dit que fest impaire si : ∀x∈A,f(−x) = −f(x).
Cela revient à dire que le graphe de fest symétrique par rapport à l’origine.
Fonction
paire
Fonction
impaire
Le graphe
d’une fonction impaire
définie en 0
passe toujours par l’origine.
En pratique Pas besoin d’étudier une fonction f:A−→ Rpaire ou impaire sur Atout entier, une étude sur A∩R+
suffit.
Définition (Périodicité) Soient T>0 et Aune partie de RT -périodique, i.e. telle que :
T
∀x∈A,x+T∈Aet x−T∈A.
Soit f:A−→ Rune fonction. On dit que fest T -périodique ou périodique de période
Tsi : ∀x∈A,f(x+T) = f(x). Le réel Test alors appelé UNE période de f .
$ATTENTION !$Une fonction périodique ne possède jamais qu’une seule période. Tout multiple entier d’une période
Test encore une période : 2T,3T,4T.. . Voilà pourquoi on ne parle jamais de « la » période, mais toujours d’UNE période.
En pratique Pas besoin d’étudier une fonction f:A−→ RT-périodique sur Atout entier, une étude sur une
période suffit, par exemple A∩[0, T[.
5