Les fonctions du collège à la terminale

1
PROGRESSIONS VERTICALES n
Les fonctions du collège à la terminale
La notion de fonction va se construire progressivement au collège dans différentes disciplines : SVT, histoire
géographie, sciences physiques et mathématiques.
En mathématiques, la construction de la notion de fonction se fait progressivement sur les quatre années du collège.
Les élèves sont amenés, dans un premier temps, à exploiter des tableaux et des graphiques, à en construire, avant de
travailler sur la notion même de fonction, en classe de 3e.
Les mathématiques comme discipline d’expression
Les mathématiques participent à l’enrichissement de l’emploi de la langue par les élèves, en particulier
par la pratique de l’argumentation. Avec d’autres disciplines, les mathématiques ont également en charge
l’apprentissage de différentes formes d’expression autres que la langue usuelle (nombres, symboles, gures,
tableaux, schémas, graphiques) ; elles participent ainsi à la construction de nouveaux langages. L’usage
largement répandu des moyens actuels de traitement de l’information et de communication exige une bonne
maîtrise de ces formes variées d’expression.
Dès la classe de 6e, les tableaux de valeurs, les lectures graphiques et la construction de représentations
graphiques illustrant une situation donnée, permettent d’appréhender cette notion et de lui donner du sens.
Cette notion deviendra une composante essentielle du lycée.
Au collège
Classe de 6e
Sciences de la vie et de la Terre
Dans les programmes apparaît déjà la construction de tableaux ou de graphiques1 :
–Origine de la matière des êtres vivants
• Objectifs scientiques
L’étude concerne la production de matière par organismes vivants et leur interdépendance alimentaire. La croissance
permet de repérer la production de matière par les organismes vivants ; c’est une des caractéristiques du vivant. Il s’agit
aussi de montrer la place particulière des décomposeurs du sol dans le recyclage des restes des organismes vivants.
• Objectifs éducatifs
Il s’agit de faire prendre conscience aux élèves de la réalité du recyclage de la matière dans leur environnement, an
d’en tenir compte dans une perspective de développement durable.
Connaissances Capacités déclinées
dans une situation d’apprentissage Commentaires
Tous les organismes vivants sont des
producteurs.
Tout organisme vivant produit sa propre
matière à partir de celle qu’il prélève dans le
milieu.
Les végétaux chlorophylliens n’ont besoin
pour se nourrir que de matière minérale, à
condition de recevoir de la lumière.
Tous les autres organismes vivants se
nourrissent toujours de matière minérale et
de matière provenant d’autres organismes
vivants.
Le sol abrite des êtres vivants qui, au travers
de réseaux alimentaires, transforment les
restes d’organismes vivants en matière
minérale : ce sont des décomposeurs.
La matière des organismes vivants se
transforme en matière minérale.
Formuler l’hypothèse d’une relation de cause
à effet entre la production de matière et le
prélèvement de matière dans le milieu.
Mesurer pour suivre les évolutions de taille et
de masse.
Construire un tableau ou un graphique pour
présenter les résultats des mesures.
Exploiter des résultats de croissance d’un être
vivant en fonction des ressources du milieu
de vie.
Suivre un protocole pour mettre en
évidence les besoins nutritifs d’un végétal
chlorophyllien.
Observer des indices an d’identier le régime
alimentaire d’un animal.
Observer différentes étapes de la
décomposition de la matière des êtres vivants.
Le rôle et la place des êtres vivants (notions
de chaînes et de réseaux alimentaires) sont
abordés à l’école élémentaire.
Les explications, toujours simples, ne
nécessitent pas le recours à une étude
détaillée des phénomènes biologiques tels que
la digestion, l’assimilation, la photosynthèse
et la minéralisation de la matière organique.
Sont exclues les notions de photosynthèse,
minéralisation et pédogenèse (formation,
structure et évolution d’un sol) ainsi que
l’étude du cycle du carbone et la mise
en évidence de la matière organique par
combustion.
On ne fera pas un inventaire systématique de
la faune du sol.
Thème de convergence : développement
durable.
1. www.education.gouv.fr/cid22120/mene08170023a.html

3
n MATHÉMATIQUES EN CLASSE DE TERMINALE
Un exemple classique consiste à représenter sur un graphique, la croissance d’un végétal en fonction du temps.
Cette approche expérimentale permet de donner du sens à ce type de représentation et d’en montrer toute la
pertinence.
Mathématiques
Dans la partie gestions de données, la résolution de problèmes a pour objectifs :
– de mettre en place les principaux raisonnements qui permettent de reconnaître et traiter les situations de
proportionnalité,
– d’initier les élèves à la présentation, à l’utilisation et à l’interprétation de données sous diverses formes
(tableaux, graphiques…).
Classe de 5e
Histoire-géographie
Il est attendu que les élèves maîtrisent certaines lectures de tableaux et de graphiques, an d’interpréter une
situation étudiée.
L’exemple de l’évolution démographique d’un pays s’y prête très bien :
Thème 2 – Les dynamiques de la population et le développement durable
Connaissances Démarches
Croissance démographique et développement
La population mondiale continue d’augmenter même si le rythme
de cette croissance se ralentit. La croissance démographique est
mise en relation avec les enjeux du développement durable, aux
différentes échelles.
Des fronts pionniers étendent le peuplement sur les marges de
certains foyers de population.
Une étude de cas au choix :
–l’Inde ;
–la Chine.
Une étude de cas au choix :
un front pionnier
–en Amérique latine,
–en Afrique.
Ces études de cas sont mises en contexte sur les planisphères
de la croissance de la population et sur celui du développement
humain.
Capacités
Localiser et situer les États les plus peuplés du monde.
Décrire l’évolution démographique de l’Inde ou de la Chine
Décrire et expliquer :
–la relation entre croissance démographique et besoins des populations ;
–un paysage d’un front pionnier.
Localiser et situer le front pionnier sur le planisphère des grands foyers de peuplement.
Identier trois grands types d’évolution démographique à partir du planisphère de la croissance démographique.
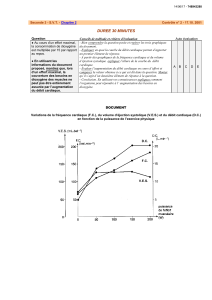
Les élèves sont alors amenés à étudier des graphiques comme celui ci-dessous qui montre l’évolution de la
population chinoise depuis 1949 :
0
200
400
600
800
1000
1200
1400
2005
2000 1995 1990 1985 1980 1975 1970 1965
1960
1955 1950
2

3
PROGRESSIONS VERTICALES n
Mathématiques
Connaissances Capacités Commentaires
1.1. Proportionnalité
Propriété de linéarité.
Tableau de proportionnalité.
Passage à l’unité ou « règle de
trois ».
– Compléter un tableau de nombres
représentant une relation de
proportionnalité, en particulier
déterminer une quatrième proportionnelle.
– Reconnaître si un tableau complet
de nombres est ou non un tableau de
proportionnalité.
Le travail sur des tableaux de nombres sans lien
avec un contexte doit occuper une place limitée.
Les activités numériques et graphiques font le plus
souvent appel à des situations mettant en relation
deux grandeurs.
Il est possible d’envisager, dans une formule, des
variations d’une grandeur en fonction d’une autre
grandeur mais toute dénition de la notion de
fonction est exclue.
Classe de 4e
Sciences physiques et chimie
L’utilisation ou la construction de graphiques apparaît de façon importante dans le programme de 4e.
Les changements d’état
Cycle de l’eau. Thème de convergence :
météorologie et climatologie
Solidication, fusion, liquéfaction, vaporisation. Réaliser, observer, schématiser des
expériences de changements d’état.
Thème de convergence :
météorologie et climatologie
Lors des changements d’état, la masse se conserve
et le volume varie.
Pratiquer une démarche expérimentale
pour mettre en évidence ces phénomènes.
Un palier de température apparaît lors du
changement d’état d’un corps pur.
Construire le graphique correspondant en
appliquant des consignes.
Contrôler, exploiter les résultats.
Thème de convergence : importance
du mode de pensée statistique
Tension continue et tension alternative périodique :
qu’est-ce qui distingue la tension fournie par le secteur de celle fournie par une pile ?
Tension continue et tension variable au cours
du temps.
Tension alternative périodique. Période.
Valeurs maximale et minimale d’une tension.
Construire le graphique représentant les variations
d’une tension au cours du temps.
En extraire des informations pour reconnaître une
tension alternative périodique, pour déterminer
graphiquement sa valeur maximale et sa période.
Décrire le comportement de la tension en fonction
du temps.
Utiliser un tableur pour recueillir, mettre en forme
les informations an de les traiter.
Poids et masse d’un corps : pourquoi un corps a-t-il un poids ?
quelle est la relation entre le poids et la masse d’un objet ?
Action à distance exercée par la Terre sur un
objet situé dans son voisinage : poids d’un corps.
Le poids P et la masse m d’un objet sont deux
grandeurs de nature différente ; elles sont
proportionnelles.
L’unité de poids est le newton (N).
La relation de proportionnalité se traduit par
P = m g
Pratiquer une démarche expérimentale pour
établir la relation entre le poids et la masse.
Construire et exploiter un graphique
représentant les variations du poids en
fonction de la masse.
Calculer, utiliser une formule.
Toute étude vectorielle (expression,
représentation) est hors programme
au collège.
Mathématiques
–Organisation et gestion de données, fonctions
Comme en classe de cinquième, le mot « fonction » est employé, chaque fois que nécessaire, en situation, et sans
qu’une dénition formelle de la notion de fonction soit donnée.
2

54
n MATHÉMATIQUES EN CLASSE DE TERMINALE
Les tableurs-grapheurs, dont l’usage a été introduit dès la classe de cinquième, donnent accès à une façon particulière
de désigner une variable : par l’emplacement de la cellule où elle se trouve dans le tableau. Cette nouveauté est un
enrichissement pour le travail sur la notion de variable, effectué sur des exemples variés.
Classe de 3e
Mathématiques
C’est en classe de 3e que la notion de fonction est formalisée pour la première fois dans l’enseignement des
mathématiques.
–Organisation et gestion de données, fonctions
L’un des objectifs est de faire émerger progressivement, sur des exemples, la notion de fonction en tant que processus
faisant correspondre, à un nombre, un autre nombre. Les exemples mettant en jeu des fonctions sont issus de situations
concrètes ou de thèmes interdisciplinaires. Les fonctions linéaires et afnes apparaissent alors comme des exemples
particuliers de tels processus. L’utilisation des expressions « est fonction de » ou « varie en fonction de », amorcée dans
les classes précédentes, est poursuivie et est associée à l’introduction de la notation f (x). L’usage du tableur grapheur
contribue aussi à la mise en place du concept, dans ses aspects numériques comme dans ses aspects graphiques. La
notion d’équation de droite n’est pas au programme de la classe de troisième.
Objectifs
La résolution de problèmes a pour objectifs :
• de synthétiser le travail conduit sur la proportionnalité dans les classes antérieures, d’approcher la notion de fonction et d’acquérir
une première connaissance des fonctions linéaires et afnes ;
• de poursuivre la mise en place de paramètres de position et de dispersion d’une série statistique ;
• d’initier à la notion de probabilité par l’étude d’exemples simples.
Connaissances Capacités Commentaires
1.1. Notion de fonction
Image, antécédent, notations
f(x), xfx7
^h
.
[Thèmes de convergence]
–Déterminer l’image d’un nombre par une
fonction déterminée par une courbe, un
tableau de données ou une formule.
–Déterminer un antécédent par lecture
directe dans un tableau ou sur une
représentation graphique.
Toute dénition générale de la notion
de fonction et la notion d’ensemble de
dénition sont hors programme.
La détermination d’un antécédent à partir
de l’expression algébrique d’une fonction
n’est exigible que dans le cas des fonctions
linéaires ou afnes.
1.2 Fonction linéaire, fonction afne
Proportionnalité.
En classe de troisième, il s’agit de
compléter l’étude de la proportionnalité
par une synthèse d’un apprentissage
commencé à l’école primaire.
Connaissances Capacités Commentaires
Fonction linéaire
Coefcient directeur de la droite
représentant une fonction linéaire.
–Déterminer par le calcul l’image d’un
nombre donné et l’antécédent d’un nombre
donné.
–Déterminer l’expression algébrique d’une
fonction linéaire à partir de la donnée d’un
nombre non nul et de son image.
–Représenter graphiquement une fonction
linéaire.
–Connaître et utiliser la relation
yax=
entre les coordonnées (x,y) d’un
point M qui est caractéristique de son
appartenance à la droite représentative de
la fonction linéaire
xax7
.
–Lire et interpréter graphiquement
le coefcient d’une fonction linéaire
représentée par une droite
L’utilisation de tableaux de
proportionnalité permet de mettre en place
le fait que le processus de correspondance
est décrit par une formulation du type « je
multiplie par a ». Cette formulation est
reliée à
xax7
.
Pour des pourcentages d’augmentation ou
de diminution, le fait que, par exemple,
augmenter de 5 % c’est multiplier par 1,05
et diminuer de 5 % c’est multiplier par 0,95
est établi.
Certains traitements des situations de
proportionnalité utilisés dans les classes
précédentes sont reliés aux propriétés
d’additivité et d’homogénéité de la
fonction linéaire.

5
PROGRESSIONS VERTICALES n
Connaissances Capacités Commentaires
Fonction afne.
Coefcient directeur et ordonnée à
l’origine d’une droite représentant une
fonction afne.
[Thèmes de convergence]
–Déterminer par le calcul l’image d’un
nombre donné et l’antécédent d’un nombre
donné.
–Connaître et utiliser la relation
yaxb=+
entre les coordonnées (x,y)
d’un point M qui est caractéristique de son
appartenance à la droite représentative de
la fonction linéaire
xaxb7+
.
–Déterminer une fonction afne à partir
de la donnée de deux nombres et de leurs
images.
–Représenter graphiquement une fonction
afne.
–Lire et interpréter graphiquement
les coefcients d’une fonction afne
représentée par une droite.
–Déterminer la fonction afne associée à
une droite donnée dans un repère.
Parmi les situations qui ne relèvent pas
de la proportionnalité, certaines sont
cependant modélisables par une fonction
dont la représentation graphique est une
droite. Cette remarque peut constituer un
point de départ à l’étude des fonctions
afnes. Pour les fonctions afnes, la
proportionnalité des accroissements de x
et y est mise en évidence.
Au lycée
Classe de seconde
L’étude des fonctions s’appuie sur les connaissances des élèves. Un travail a été mené pour faire émerger un
processus faisant correspondre un nombre à un autre nombre, les fonctions linéaires et afnes étant étudiées
comme des cas particuliers.
D’après le document ressource fonctions seconde, http://cache.media.eduscol.education.fr/le/
Programmes/18/1/Doc_ressource_fonctions_109181.pdf, l’objectif est de rendre les élèves capables d’étudier :
– un problème se ramenant à une équation du type fx k
=
^h
et de le résoudre dans le cas où la fonction est
donnée (dénie par une courbe, un tableau de données, une formule) et aussi lorsque toute autonomie est
laissée pour associer au problème divers aspects d’une fonction ;
– un problème d’optimisation ou un problème du type fx k
2
^h
et de le résoudre, selon les cas, en
exploitant les potentialités de logiciels, graphiquement ou algébriquement, toute autonomie pouvant être
laissée pour associer au problème une fonction. Les situations proposées dans ce cadre sont issues de
domaines très variés : géométrie plane ou dans l’espace, biologie, économie, physique, actualité, etc. Les
logiciels mis à la disposition des élèves (tableur, traceur de courbes, logiciels de géométrie dynamique,
de calcul numérique, de calcul formel, etc.) peuvent être utilement exploités. Par ailleurs, la résolution de
problèmes vise aussi à progresser dans la maîtrise du calcul algébrique et à approfondir la connaissance
des différents types de nombres, en particulier pour la distinction entre un nombre et ses valeurs
approchées.
Il s’agit également d’apprendre aux élèves à distinguer la courbe représentative d’une fonction des dessins
obtenus avec un traceur de courbe ou comme représentation de quelques données. Autrement dit, il s’agit
de faire comprendre que des dessins peuvent sufre pour répondre de façon satisfaisante à un problème
concret mais qu’ils ne sufsent pas à démontrer des propriétés de la fonction.
Le programme encourage une programmation moins centrée sur les notions elles-mêmes mais davantage sur la
nature des problèmes que les élèves doivent savoir résoudre. Par exemple, au niveau du tr avail à conduire sur le sens
de variation des fonctions, l’objectif n’est pas de centrer l’apprentissage sur la maîtrise du « comment étudie-t-on
en général le sens de variation d’une fonction dénie par une expression algébrique ? ». Il s’agit davantage d’obtenir
que les élèves donnent sens à ce qu’est une fonction croissante (ou décroissante) sur un intervalle et sachent, quand
le sens de variation d’une fonction est connu, comment exploiter une telle information pour répondre à une question.
L’attendu est aussi qu’ils soient capables, pour résoudre un problème, de donner de façon autonome le sens
de variation d’une fonction trinôme du second degré. Dans le cadre d’une différenciation pédagogique, on peut
s’autoriser à ce que quelques élèves deviennent capables d’aller au-delà et il est même souhaitable de le faire.