I Équation d`une droite

Seconde Droites et systèmes 2011-2012
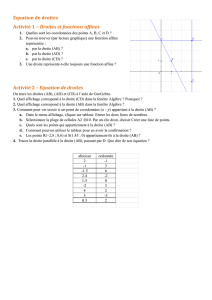
I Équation d’une droite
I.1 Activité d’introduction
Lien vers l’activité : http://www.michelimbert.fr/IMG/pdf/versequation2droite.pdf
L’équation d’une droite est le lien exclusif qui existe entre les coordonnées xet ydes points de la droite.
Exemple 1 Si y= 2x+ 3 est l’équation d’une droite ddans un repère (O;I;J), les points de la droite dont une ordonnée égale à
deux fois leur abscisse plus trois et ce sont les seuls à avoir cette propriété. (les points qui ne sont pas sur la droite ne la vérifient pas)
I.2 Différents types d’équations
Propriété :
1. Toute droite parallèle à l’axe des ordonnées a une équation de la forme x=coù cest un réel.
Tous les points de la droite ont une abscisse égale à cet ce sont les seuls.
2. Toute droite du plan non parallèle à l’axe des ordonnées à une équation de la forme y=ax +boù aet bsont
des nombres réels.
Tous les points de la droite ont une ordonnée égale à a« fois » l’abscisse plus bet ce sont les seuls.
Remarque 1 Dans le cas 2., si a= 0, l’équation se réduit à y=bet la droite est parallèle à l’axe des abscisses.
Tous les points de la droite ont une ordonnée égale à bet ce sont les seuls.
OI
J
c
OI
J
b
OI
J
b
Remarque 2 :
Une expression de la forme ax +by +c= 0 avec a, b et créels est aussi l’équation d’une droite. Pour s’en convaincre, la
technique consiste à « isoler » xou ypour se ramener aux équations vues plus haut que l’on appelera équations réduites .
EXERCICE 1 :
Transformer les équations suivantes en équations réduites :
2x−3y+ 1 = 0 ; 9 −5y= 0 ; 3x+ 8 = 0 ; x2+ 2y−1 = 0
I.3 lien entre droite et fonction affine
Une fonction affine fest de la forme f(x) = ax +b. Sa représentation graphique admet une équaiton de la forme
y=ax +b. Donc :
Propriété 1 Toute fonction affine a pour représentation graphique une droite non parallèle à l’axe des ordonnées
EXERCICE 2 :
Représenter dans le repère ci-contre la droite représentant la fonction affine f
définie par :
f:x7−→ −2x+ 1.5
OI
J
My Maths Space 1 sur 3

Seconde Droites et systèmes 2011-2012
Vocabulaire 1 :
Dans l’équation d’une droite non parallèle à l’axe des ordonnées y=ax +b,as’appelle le coefficient directeur et bs’appelle
l’ordonnée à l’origine.
Conséquence : Si l’on connaît les coordonnées de deux points A(xA;yA) et B(xB;yB), le coefficient directeur a
est donné par la formule suivante :
a=yA−yB
xA−xB
(les « ysur les x» )
I.4 Détermination pratique de l’équation d’une droite passant par 2 points
On connaît dans un repère (O;I;J), les coordonnées A(xA;yA) et B(xB;yB).
1. Si xA6=xBalors la droite coupe l’axe des ordonnées et si yA6=yB, elle n’est pas parallèle à l’axe des abscisses :
on est dans le cas général.
2. On cherche le coefficient directeur aavec la formule vue plus haut ;
3. On dispose de adonc dans l’équation y=ax +b, seul best inconnu. Avec les coordonnées de Aou celles de B,
en remplaçant dans l’équation, on trouve b.
EXERCICE 3 :
Dans le repère ci-contre, on considère les points A(−1; 2) et B(4; −2) Déter-
miner l’équation de la droite (AB).
OI
J
I.5 Droites parallèles
Théorème 1 Deux droites non parallèles à l’axe des ordonnées sont parallèles si et seulement si elles ont le même
coefficient directeur
Exemple 2 1. Les droites d’équations y=−2x+ 4 et y=−2x+πsont parallèles car elles ont le même coefficient directeur.
2. Quelle est l’équation réduite de la droite d1parallèle à d2:y=−
1
2x+ 3 passant par (0; −1.5) ?
3. Les droites d3et d4d’équations respectives 2x−3y= 4 et 3x−5y+ 2 = 0 sont-elles parallèles ?
II Systèmes Linéaires
II.1 Définition
Définition 1 Un système linéaire de deux équations à deux inconnues est un système de la forme :
ax +by =c
a′x+b′y=c′où a, b, c, a′, b′, c′sont des réels et (x;y)est le couples des inconnues.
My Maths Space 2 sur 3

Seconde Droites et systèmes 2011-2012
Remarque 3 :
•Être solution d’un système, c’est être un couple de nombres vérifiant les équations du système (2 ou plus).
Le couple (−1; 2) est-il solution du système 2x−4y=−10
x+ 2y= 3 ?
•Résoudre un système, c’est trouver toutes les solutions du système.
Le système précédent est-il résolu ?
II.2 Nombre de solutions d’un système
Soit (O;I;J) un repère.
Lien graphique : Une équation linéaire à deux inconnues est assimilable à une équation de droite. Un couple
solution d’une équation linéaire est un couple de coordonnées d’un point de la droite.
(x0;y0) solution de ax +by =c⇔La droite d’équation ax +by =cpasse par le point de coordonnées (x0;y0)
Exemple 3 :
(−2; 3) est solution de ......................
OI
J
Généralisation : (x0;y0) est solution d’un système ax +by =c
a′x+b′y=c′⇔Le point de coordonnées (x0;y0) appar-
tient aux droites det d′d’équations respectives ax +by =cet a′x+b′y=c′. D’où le théorème suivant :
Théorème 2 :
det d′sont sécantes :
un seul couple solution
O
I
J
d
d′
det d′sont parallèles :
pas de couple solution
OI
J
d
d′
det d′sont confondues :
Une infinité de couples solutions
OI
J
d
d′
Exemple 4 Résoudre le système suivant : 2x+ 3y= 4
5x+ 6y= 7
My Maths Space 3 sur 3