2. Fiche de révisions sur les droites - Cours Première S2

Révisions de 2nde
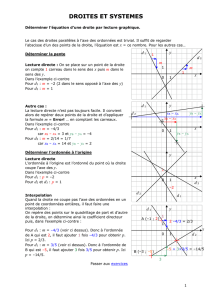
Equation d’une droite
Première S
Toute droite non parallèle à l’axe des ordonnées est un ensemble de points M dont les coordonnées vérifient
une équation du type y = mx + p, où m et p sont des réels fixés.
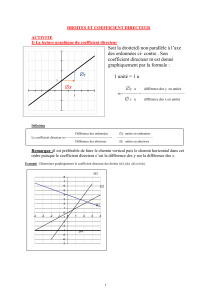
 m est appelé le coefficient directeur de la droite. Il détermine la direction (« inclinaison ») de la droite.
 p est l’ordonnée à l’origine (c'est-à-dire l’ordonnée du point de la droite qui a pour abscisse zéro)
Remarque : On retrouve l’équation d’une fonction affine du type f( x ) = a x + b, qui est représentée par… une
droite !
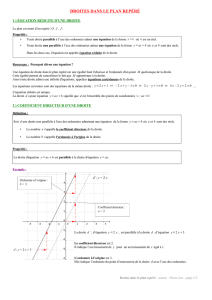
Toute droite parallèle à l’axe des ordonnées est un ensemble de points M dont les coordonnées vérifient une
équation du type x = c où c est un réel fixé.
Coefficient directeur d’une droite du type y = mx + p:
Soit A(xA ; yA) et B(xB ; yB). Le coefficient directeur de la droite (AB) est : m = yB – yA
xB – xA
Exemple :
Soit A(2 ; 3) et B(4 ; -5). On veut déterminer l’équation (du type y = mx + p) de la droite (AB)
1 On calcule le coefficient directeur de la droite :
m = yB – yA
xB – xA
= -5 – 3
4 – 2
= -8
2
= -4
On en déduit que (AB) :
4y x p  
2 On remplace m par sa valeur, et x et y par les
coordonnées de A (ou B) dans une des équations :
4y x p  
3 = (-4)  2 + p
 3 = -8 + p
 3 + 8 = p
 p = 11
L’équation de la droite (AB) est donc : y = -4x + 11
Théorème : Deux droites sont parallèles si et seulement si leurs coefficients directeurs sont égaux.
Exemple :
Soient les droites : (d1) : y = 2x + 5 (d2) : y = -3x + 5 (d3) : y = -2x – 3 et (d4) : y = 2x – 3
On compare les coefficients directeurs des droites. On peut dire que les droites (d1) et (d4) sont parallèles.
Construire une droite dans un repère:
Exemples :
Cas 1 : Construisons la droite (d1) : y = 2x + 5
Cas 2 : On veut tracer la droite passant par le point
A( 1 ; - 2) et de coefficient directeur 2