Travail proposé en Mathématiques

Page 1 sur 6!
"#$%&'(%!")*!+!,-#.(/0%12-(3(%!+!456-7356(/0%.!
!
!
,&8'&533%!9%!356-7356(/0%.!%$!:;&%!")*<=!
!
• >/056(8$!90!.%?8$9!9%'&7@!9(.?&(3($5$6!A!
• B83C&%!97&(D7!9E0$%!F8$?6(8$!%$!0$!G8($6!A!
• )5$'%$6%!H!I5!?80&C%!&%G&7.%$656(D%!9E0$%!
F8$?6(8$!%$!0$!G8($6!8J!%II%!97&(D5CI%!A!
• K8$?6(8$!97&(D7%!A!
• L(%$!%$6&%!.('$%!9%!I5!97&(D7%!%6!.%$.!9%!D5&(56(8$!A!
• >M6&%303!9E0$%!F8$?6(8$N!!
!
!
!"#$%&'()*+,-./.
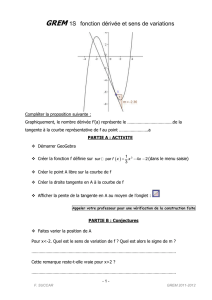
O!G5&6(&!9%.!&%I%D7.!8C6%$0.!%6!9%!3897I(.56(8$.!G5&!9%.!F8$?6(8$.@!?833%$6!
976%&3($%&!I5!D(6%..%!H!G5&6(&!9E0$%!3897I(.56(8$!90!97GI5?%3%$6!%6!IE5??7I7&56(8$!H!
G5&6(&!9E0$%!3897I(.56(8$!9%!I5!D(6%..%!9%!I5!D8(60&%N!!
!
!
01"-.2(")*-./.3*)-44-.-).)(56-5)-.
,80&!3%$%&!0$%!7609%!356-7356(/0%!9%!I5!9(.65$?%!G5&?80&0%!%$6&%!:!.!%6!P!.@!8$!
3897I(.%!.0&!?%6!($6%&D5II%!9%!6%3G.!I5!9(.65$?%!G5&!0$%!F8$?6(8$!𝑑!97F($(%!G5&!Q!
!
𝑑𝑡=−0,423!𝑡!+!3,29𝑡!−2,43𝑡!!!!!!!!pour!1≤𝑡≤4!
!
L5!9(.65$?%!G5&?80&0%!%.6!%MG&(37%!%$!3;6&%.N!
!
:N OD%?!I%!I8'(?(%I!R78'7C&5@!6&5?%&!I5!&%G&7.%$656(8$!'&5G-(/0%!9%!I5!F8$?6(8$!𝑑!.0&!
IE($6%&D5II%![1;4]N!
,I5?%&!I%!G8($6!O!9E5C.?(..%!2!5GG5&6%$5$6!H!I5!?80&C%!&%G&7.%$65$6!I5!F8$?6(8$!𝑑N!
<N 28$.6&0(&%!0$!?0&.%0&!𝑐1!G&%$5$6!9%.!D5I%0&.!9%!−1!H!1!5D%?!0$!($?&73%$6!9%!
0,01N!!
,I5?%&!I%!G8($6!𝐵!9E5C.?(..%!2+𝑐1!5GG5&6%$5$6!H!I5!?80&C%!9%!I5!F8$?6(8$!𝑑N!
)&5?%&!I5!9&8(6%!(𝐴𝐵)N!
SN 25I?0I%&!𝑑(2)!%6!𝑑(2,5)N!T0%!&%G&7.%$6%$6!?%.!$83C&%.!U!
PN 25I?0I%&!I%!$83C&%!!!,!!!(!)
!,!!!N!
,8.(6(8$$%&!𝑐1!.0&!I5!D5I%0&!0,5N!T0%!&%G&7.%$6%!?%!$83C&%!G80&!I5!9&8(6%!(𝐴𝐵)!U!
>$!98$$%&!0$%!($6%&G&7656(8$!G-#.(/0%!G80&!I5!D8(60&%N!
VN 25I?0I%&!I%!$83C&%!!!,!" !!(!)
!,!"!!N!
*$6%&G&76%&!'78376&(/0%3%$6!?%!$83C&%!%6!%$!98$$%&!0$%!($6%&G&7656(8$!
G-#.(/0%N!
WN =5$.!I5!F%$X6&%!Calcul&formel&du&logiciel&Géogébra@!%MG&(3%&!I%!/086(%$6!!
𝑑2+ℎ−𝑑(2)
ℎ!
%$!F8$?6(8$!9%!ℎN!

Page 2 sur 6!
L8&./0%!ℎ!.%!G&%$9!9%.!D5I%0&.!9%!GI0.!%$!GI0.!G&8?-%!9%!0@!/0%II%!D5I%0&!G&%$9!
I%!/086(%$6!Q!
𝑑2+ℎ−𝑑(2)
ℎ!
!
Ce!nombre!est!appelé!nombre!dérivé!de!la!fonction!𝒅!en!𝟐.!
!
En!terme!concret,!cette!valeur!correspond!à!la!vitesse!instantanée!de!la!
voiture!à!l’instant!𝒕=𝟐.!
!
YN K5(&%!D5&(%&!I%!?0&.%0&!𝑐1!G80&!I%!&5GG&8?-%&!9%!0N!
T0%II%!G8.(6(8$!G&%$9!I5!9&8(6%!(𝐴𝐵)!U!!
T0%I!%.6!.8$!?8%FF(?(%$6!9(&%?6%0&!U!
ZN 283G5&%&!I%.!&7.0I656.!9%.!9%0M!/0%.6(8$.!G&7?79%$6%.N!
!
7-.5#'$"-.8&"*9&.8-.%(.:#5;)*#5.𝒅.-5.𝟐.-4).&6(%.;#-::*;*-5).8*"-;)-,".8-.%(.
)(56-5)-.<.%(.;#,"$-."-2"&4-5)(5).%(.:#5;)*#5.𝒅.(,.2#*5).8=($4;*44-.𝟐>.
!
[N =%!I5!3X3%!35$(;&%@!976%&3($%&!'&5G-(/0%3%$6!I%!$83C&%!97&(D7!9%!I5!F8$?6(8$!
𝑑!%$!SN!!
>$!9790(&%!I5!D(6%..%!($.65$65$7%!9%!I5!D8(60&%!H!IE($.65$6!𝑡=3N!
!
!
?1'-.2(")*-./.@#8&%*4()*#5.8-.%(.9*)-44->.
,80&!3%$%&!0$%!7609%!356-7356(/0%!9%!I5!D(6%..%!%$6&%!\!.!%6!P!.@!8$!3897I(.%!
.0&!?%6!($6%&D5II%!9%!6%3G.!I5!D(6%..%!G5&!0$%!F8$?6(8$!𝑣!97F($(%!9%!I5!35$(;&%!
.0(D5$6%!Q!
𝑣𝑡=−1,27!𝑡!+!6,57𝑡−2,43!!!!!pour!0,6≤𝑡≤4!
!
L5!D(6%..%!%.6!%MG&(37%!%$!3N.1:N!
!
!
:N O!IE5(9%!90!I8'(?(%I!R78'7C&5@!6&5?%&!I5!
?80&C%!&%G&7.%$65$6!I5!F8$?6(8$!𝑣!.0&!
IE($6%&D5II%![0,6;4]N!
!
<N =76%&3($%&!I5!D(6%..%!35M(35I%!𝑣!"#!
566%($6%!G5&!I%!D7-(?0I%!95$.!?%6!
($6%&D5II%!9%!6%3G.!%6!G&7?(.%&!50!C806!9%!
?83C(%$!9%!6%3G.!%II%!%.6!566%($6%N!
!
!
SN ]%6&80D%&!?%.!&7.0I656.!G5&!I%!?5I?0IN!
!
!
PN "0&!/0%I!($6%&D5II%!9%!6%3G.!I5!D(6%..%!%.61%II%!.0G7&(%0&%!H!P!3N.1:!U!
^$!$86%&5!𝑡!!.5!C8&$%!($F7&(%0&%!%6!𝑡!!.5!C8&$%!.0G7&(%0&%N!!
283C(%$!9%!6%3G.!I5!D(6%..%!&%.6%161%II%!.0G7&(%0&%!H!4!3N.1:!U!
_7&(F(%&!'&5G-(/0%3%$6N. .
\@\!
:@\!
<@\!
S@\!
P@\!
V@\!
W@\!
Y@\!
\@W\!
\@[\!
:@<\!
:@V\!
:@Z\!
<@:\!
<@P\!
<@Y\!
S@\\!
S@S\!
S@W\!
S@[\!
A#,"$-.#$)-5,-.(9-;.,5.)($%-,".
_(6%..%!

Page 3 sur 6!
B1'-.2(")*-./.C5-.5#,9-%%-.:#5;)*#5./.%(.:#5;)*#5.8&"*9&->.
^$!5!D0!/0%!/0E%$6&%!\@W!%6!P!.%?8$9%.@!I5!D(6%..%!G%06!X6&%!3897I(.7%!G5&!
I5!F8$?6(8$!Q!
𝑣𝑡=−1,27!𝑡!+!6,57𝑡−2,43!!!!!pour!0,6≤𝑡≤4!
!
7(.9*)-44-.-4).#$)-5,-.;#''-.%(.9("*()*#5.8,.8&2%(;-'-5).4,".,5.
*5)-"9(%%-.8-.)-'24>.
D-.%(.'E'-.'(5*1"-F.%=(;;&%&"()*#5.-4).#$)-5,-.;#''-.%(.9("*()*#5.8-.%(.
9*)-44-.4,".,5.*5)-"9(%%-.8-.)-'24>.
!
:N 2&7%&!0$!?0&.%0&!𝑐2!G&%$5$6!9%.!D5I%0&.!9%!0,6!H!4!5D%?!0$!($?&73%$6!9%!0,01N!
,I5?%&!I%!G8($6!!𝑀!9%!?88&98$$7%.!!𝑐2,𝑣(𝑐2)!
)&5?%&!I5!65$'%$6%!50!G8($6!𝑀!H!I5!?80&C%!&%G&7.%$65$6!!𝑣!%6!97F($(&!.5!G%$6%N!
]%$833%&!I5!G%$6%!𝑝N!
<N O!IE5(9%!90!I8'(?(%I!R78'7C&5@!!
5N 976%&3($%&!'&5G-(/0%3%$6!I5!D(6%..%!H!𝑡=2!.N!
CN 976%&3($%&!'&5G-(/0%3%$6!IE5??7I7&56(8$!H!𝑡=2!.N!
?N 976%&3($%&!'&5G-(/0%3%$6!IE5??7I7&56(8$!I8&./0%!I5!D(6%..%!%.6!9%!4!3N.1:!
?E%.61H19(&%!G80&!𝑡!!%6!!𝑡!!8C6%$0.!G&7?79%33%$6N!!
T0%!&%35&/0%1618$!U!2833%$6!G%0618$!I%!`0.6(F(%&!U!
!
G5.4=*5)&"-44-.'(*5)-5(5).<.%(.:#5;)*#5.+,*.<.𝒕.(44#;*-.%=(;;&%&"()*#5.8-.%(.
9#*),"-.<.;-).*54)(5)F.;=-4)H<H8*"-.<.%(.:#5;)*#5.+,*.<.).(44#;*-.%-.;#-::*;*-5).
8*"-;)-,".8-.%(.)(56-5)-.<.%(.;#,"$-."-2"&4-5)(5).%(.9*)-44->.
!
SN ,I5?%&!I%!G8($6!𝐴!9%!?88&98$$7%.!(𝑐2,𝑝)!9%!I5!65$'%$6%!%6!5?6(D%&!I5!6&5?%!90!
G8($6!𝐴N!
PN K5(&%!D5&(%&!I%.!D5I%0&.!G&(.%.!G5&!I%!?0&.%0&!𝑐2!%6!
8C.%&D%&!I5!F%$X6&%!'&5G-(/0%!Q!I5!?80&C%!/0(!5GG5&5a6!
%.6!I5!?80&C%!9%!I5!F8$?6(8$!5??7I7&56(8$N!
!
I5.'()J&'()*+,-F.;-))-.:#5;)*#5.-4).(22-%&-.
:#5;)*#5.8&"*9&->.
!
La!fonction!accélération!est!la!dérivée!de!la!
fonction!vitesse.!
!
!
K1'-.2(")*-./.L-54.8-.9("*()*#5.8-.%(.:#5;)*#5.-).4*65-.8-.
%(.:#5;)*#5.8&"*9&->.
!
:N =76%&3($%&!'&5G-(/0%3%$6!I5!D5I%0&!9%!IE5??7I7&56(8$!
I8&./0%!I5!D(6%..%!%.6!35M(35I%N!
<N =&%..%&!I%!65CI%50!9%!D5&(56(8$!9%!I5!F8$?6(8$!D(6%..%!
.0&!IE($6%&D5II%![0,6;4]N!
SN =&%..%&!I%!65CI%50!9%!.('$%.!9%!I5!F8$?6(8$!
5??7I7&56(8$!.0&!IE($6%&D5II%![0,6;4]N!
PN ,%0618$!765CI(&!0$!I(%$!%$6&%!?%.!9%0M!&7.0I656.!U!
O&'03%$6%&!I5!&7G8$.%N!
K('0&%!&75I(.7%!5D%?!R78'7C&5!

Page 4 sur 6!
M1'-.2(")*-./.N-)#,".(,O.8#55&-4.-5"-6*4)"&-4.4,".%(.;(")-.LD>.
_8(?(!9%0M!'&5G-(/0%.!8C6%$0.!H!G5&6(&!9%.!98$$7%.!9%!I5!F%0(II%!9%!?5I?0IN!
!
!
!
:N ]%G7&%&!I%.!G-5.%.!9E5??7I7&56(8$@!9%!97?7I7&56(8$b!
<N =&%..%&!I%!65CI%50!9%.!D5&(56(8$.!9%!I5!F8$?6(8$!D(6%..%N!
SN =&%..%&!I%!65CI%50!9%!.('$%.!9%!I5!F8$?6(8$!5??7I7&56(8$N!
PN L%.!&7.0I656.!.8$61(I.!?8-7&%$6.!U!
! !
1P@\!
1S@\!
1<@\!
1:@\!
\@\!
:@\!
<@\!
S@\!
P@\!
V@\!
W@\!
Y@\!
\@S!
\@[!
:@V!
<@:!
<@Y!
S@S!
S@[!
P@V!
V@:!
V@Y!
W@S!
W@[!
Y@V!
Z@:!
Z@Y!
[@S!
[@[!
:\@V!
::@:!
::@Y!
:<@S!
:<@[!
:S@V!
:P@:!
D(6%..%!
5??7I7&56(8$!

Page 5 sur 6!
O$$%M%!:!
!
brut
brut
brut
brut
brut
brut
brut
Force
ACC
ACC
s
m
m/s
Km/h
m.s-²
Dist
Ualim
Upile
Ubat
Ialim
Ipile
Ibat
F
X
Y
Temps
Distance
Vitesse
Vitesse
Accé
0,0
0
0
0"
946"
736"
948"
511"
508"
522"
0"
320"
329"
0,1"
0,00"
0,0"
0,0"
0,0"
0"
950"
696"
949"
510"
514"
519"
0"
316"
330"
0,2"
0,00"
0,0"
0,0"
0,0"
0"
950"
696"
949"
510"
514"
519"
0"
318"
330"
0,3"
0,00"
0,0"
0,0"
0,0"
0"
951"
696"
950"
511"
514"
517"
0"
315"
328"
0,4"
0,00"
0,0"
0,0"
0,5"
0"
950"
696"
951"
510"
513"
518"
0"
318"
331"
0,5"
0,00"
0,0"
0,0"
2,1"
2"
531"
486"
590"
884"
521"
904"
0"
430"
329"
0,6"
0,03"
0,3"
1,0"
3,7"
10"
542"
489"
606"
911"
516"
915"
0"
449"
355"
0,7"
0,13"
1,1"
3,8"
5,3"
24"
597"
512"
632"
919"
528"
902"
0"
431"
345"
0,8"
0,32"
1,9"
6,7"
5,9"
44"
634"
532"
673"
890"
527"
861"
0"
416"
341"
0,9"
0,59"
2,7"
9,6"
6,4"
66"
672"
552"
703"
843"
524"
819"
0"
393"
346"
1,0"
0,88"
2,9"
10,5"
5,9"
92"
703"
566"
727"
796"
524"
784"
0"
390"
363"
1,1"
1,22"
3,5"
12,4"
4,8"
122"
730"
580"
752"
763"
522"
750"
0"
379"
380"
1,2"
1,62"
4,0"
14,4"
4,3"
154"
747"
591"
769"
738"
522"
733"
0"
368"
370"
1,3"
2,05"
4,3"
15,3"
3,7"
190"
767"
600"
787"
712"
519"
708"
0"
349"
290"
1,4"
2,53"
4,8"
17,2"
3,2"
226"
779"
608"
797"
703"
521"
694"
0"
344"
254"
1,5"
3,01"
4,8"
17,2"
2,1"
264"
792"
614"
810"
688"
519"
679"
0"
344"
251"
1,6"
3,51"
5,1"
18,2"
2,1"
302"
802"
620"
819"
671"
519"
667"
0"
339"
215"
1,7"
4,02"
5,1"
18,2"
1,6"
342"
806"
621"
820"
669"
519"
663"
0"
346"
278"
1,8"
4,55"
5,3"
19,2"
1,1"
384"
819"
627"
831"
653"
519"
648"
0"
352"
354"
1,9"
5,11"
5,6"
20,1"
1,6"
424"
824"
631"
836"
644"
519"
644"
0"
330"
379"
2,0"
5,64"
5,3"
19,2"
1,6"
468"
830"
635"
844"
638"
518"
634"
0"
336"
402"
2,1"
6,22"
5,9"
21,1"
1,1"
512"
838"
640"
849"
629"
519"
627"
0"
326"
397"
2,2"
6,81"
5,9"
21,1"
0,5"
556"
841"
640"
853"
626"
517"
624"
0"
330"
373"
2,3"
7,39"
5,9"
21,1"
1,6"
600"
847"
644"
859"
614"
516"
614"
0"
334"
390"
2,4"
7,98"
5,9"
21,1"
0,5"
646"
855"
646"
863"
610"
518"
608"
0"
321"
416"
2,5"
8,59"
6,1"
22,0"
0,0"
692"
884"
661"
889"
562"
516"
566"
0"
320"
382"
2,6"
9,20"
6,1"
22,0"
0,0"
736"
924"
681"
925"
511"
513"
516"
0"
310"
386"
2,7"
9,79"
5,9"
21,1"
0,0"
780"
933"
687"
932"
511"
515"
515"
0"
288"
371"
2,8"
10,37"
5,9"
21,1"
-1,1"
824"
935"
690"
934"
510"
515"
516"
0"
284"
324"
2,9"
10,96"
5,9"
21,1"
-1,1"
866"
930"
687"
933"
510"
514"
522"
0"
283"
307"
3,0"
11,52"
5,6"
20,1"
-0,5"
908"
937"
687"
934"
511"
515"
516"
0"
288"
293"
3,1"
12,08"
5,6"
20,1"
-1,6"
950"
934"
689"
933"
513"
515"
519"
0"
280"
261"
3,2"
12,64"
5,6"
20,1"
-1,6"
988"
935"
690"
937"
511"
514"
517"
0"
286"
226"
3,3"
13,14"
5,1"
18,2"
-1,6"
1026"
937"
690"
939"
511"
514"
516"
0"
284"
216"
3,4"
13,65"
5,1"
18,2"
-1,6"
1062"
938"
691"
939"
510"
515"
517"
0"
275"
218"
3,5"
14,12"
4,8"
17,2"
-2,1"
1098"
938"
691"
939"
509"
514"
517"
0"
283"
214"
3,6"
14,60"
4,8"
17,2"
-1,6"
1132"
933"
689"
935"
519"
514"
522"
0"
284"
197"
3,7"
15,06"
4,5"
16,3"
-2,1"
1164"
934"
690"
936"
515"
515"
522"
0"
285"
206"
3,8"
15,48"
4,3"
15,3"
-1,6"
1194"
937"
691"
936"
515"
516"
521"
0"
293"
207"
3,9"
15,88"
4,0"
14,4"
-2,7"
1224"
939"
691"
939"
512"
514"
520"
0"
286"
449"
4,0"
16,28"
4,0"
14,4"
-2,1"
!